UERJ, Sem Campus, Cálculo I, Listas de Cálculo 1 - UERJ - Lista 1, Questão 4e
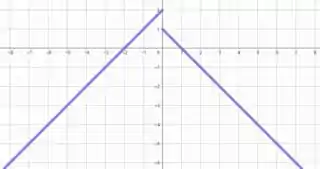
4. Encontre o domínio e esboce o gráfico da função.
e)
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema, queremos obter o domínio e o esboço do gráfico da função definida por partes .
Parece tranquilo? 🤔
Para obter o domínio de uma função, podemos fazer uma analogia com uma receita de uma pizza...
Em uma receita, adicionamos os ingredientes na massa e levamos ao forno.
O domínio de uma função é todos os valores possíveis que a função pode adquirir na variável, ou seja, os possíveis valores para . Assim como os ingredientes da pizza pode ser considerado como o domínio da pizza.
Já para obter o gráfico de uma função, podemos obter alguns pontos dela e estimar o comportamento da função entre os pontos.
Sacou? Bora começar! 😁
Passo 2
Primeiro vamos obter o domínio de , pra isso, vamos analisar a função.
Na função , vemos tanto para quanto para não há restrições para valores de .
Portanto, o domínio de são todos os valores reais.
Legal, né? 😎
Passo 3
Agora para esboçar o gráfico da função, vemos que para a função vai ter um comportamento e para a função terá outro comportamento.
Para ambos os casos, temos que será um polinômio de primeiro grau, ou seja, uma reta.
Para , a reta será dada por , ou seja, a reta crescente que corta em no eixo e em no eixo .
Já para , a reta é dada por , ou seja, a reta corta o eixo em e o eixo em ...
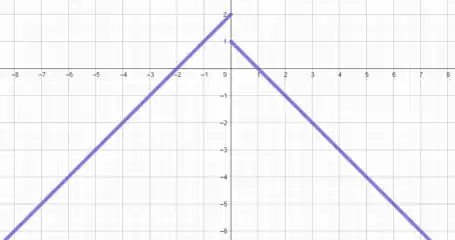
Sacou como faz? Responde Aí! 😉
Resposta
