O volume do domínio da função é
a.
b.
c.
d.
e.
f.
g. 16
h. 4
Passo 1
Fala galera, beleza? Bora resolver o nosso exercício? Vamos lá.
Primeiro, o que seria o domínio de uma função? São todos os valores possíveis que as variáveis daquela função podem ter, então a gente precisa analisar se existem restrições.
O numerador de uma fração pode ter qualquer valor, então a gente pode analisar direto cada termo do numerador.
Vamos começar analisando . Como temos uma raiz, ela tem que ser maior ou igual a 0, então:
Agora vamos analisar . Assim como no de cima, ela tem que ser maior ou igual a 0:
Passo 2
Ok, agora, vamos analisar o denominador. No caso, temos que lembrar que o denominador tem que ser diferente de zero pois não podemos dividir nada por zero.
E ai que entra algo muito legal. O nosso denominador vai ser sempre maior do que zero. Por que? Pois nós temos 2 raizes somando ainda com o 4, e como nós vimos la no passo 1, as raízes tem que ser maiores ou igual a zero. Se as raízes forem iguais a zero, vamos ter 4 + 0 + 0 = 4. Show?
Beleza, então já confirmamos que o denominador vai ser sempre maior do que zero, agora vamos ter que analisar as restrições de cada termo.
Vamos pegar primeiro o :
Agora vamos para o termo :
Passo 3
Beleza galera, vamos analisar aqui tudo o que conseguimos encontrar
Reparem que se a gente for olhar as coordenadas, nós vamos ter uma base quadrada em função do x e y, com lado igual a 4 (pois de -2 até +2 há uma diferença de 4 unidades)
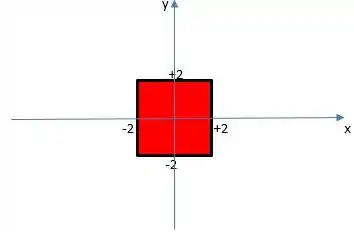
E vamos ter uma altura em função de z igual a 2 (pois de -1 ate +1 há uma diferença de 2 unidades):
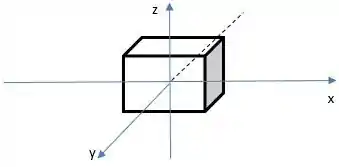
Se a gente for calcular esse volume, vamos usar a regra básica:
É isso, acabamos? NÃÃO. Temos uma condição que não podemos ignorar que foi determinada lá no Passo 1:
Então precisamos determinar quando que
Passo 4
Muito bem, vamos analisar todos os cenários possíveis quando temos o produto de 3 variáveis. Lembrando que cada variável pode ou ser positiva ou negativa:
Se a gente for reparar no nosso esquema, as únicas combinações que satisfazem a nossa condição vão ser:
Olha que interessante. Temos um total de 8 combinações possíveis e dessas 8, metade satisfazem a condição, certo? Se o volume total que a gente calculou no passo anterior seria com as 8 combinações, metade das combinações vão representar metade do volume. Então: