UFSCar; Cálculo I – 1ª Lista de exercícios - Revisão de funções – Ex. 2c
2) Determine o domínio e esboce o gráfico das funções
c)
Passo 1
Bomm dia, boa tarde, boa noiteee pessoas lindas!! Se vocês estão perdidinhos nessa questão, caíram no lugar certo. É aqui que vamos resolver ela da maneira mais tranquila possível, igual esse patinho no balanço dele.
Uhuul, bora lá então!
Nesse exercício precisamos encontrar o domínio e construir o gráfico da função dada pelo enunciado.
Legal, mas o que é domínio de uma função? E como se constrói um gráfico?
Bem, para entendermos o que é um domínio, precisamos definir o que é função. Conhecemos como função uma relação entre dois conjuntos A e B em que, para todo elemento do conjunto A, existe um único correspondente no conjunto B. A “ferramenta” que transforma os elementos do conjunto A em um elemento do conjunto B é o que chamamos de função.
Assim já definimos quem é o domínio. O domínio é o conjunto numérico formado pelos valores que pode assumir na nossa função.
Já para a construção do gráfico, usaremos métodos específicos para cada função, levando em consideração algumas simplificações possíveis e características do grau e forma da função.
Muito legal, não é? Então bora calcular!
Passo 2
Como vimos no Passo 1, o domínio é formado pelos possíveis valores de . Aqui procuramos se há algum valor de que torna a função impossível de ser resolvida.
E aqui vai uma dica valiosa! Como temos uma fração na nossa função, precisamos avaliar o denominador. Ele nunca poderá ser !
Então:
Aqui já temos um valor que não está no domínio dessa função.
Além disso, avaliaremos o numerador para tentar encontrar algum outro possível valor que torna a função impossível.
Porém, em todos os valores reais servem.
Então o domínio será todos os números reais, exceto :
Passo 3
Agora, para o gráfico, vamos começar identificando qual é o tipo dessa função.
Com certeza você já deve ter percebido que há um produto notável no nosso numerador.
Isso mesmo!
Reescrevendo a função:
Agora podemos simplificar:
Ou seja, simplificamos a nossa função para descobrirmos que ela é uma função de primeiro grau. E assim definimos, também, que nosso gráfico será uma reta!
E para desenhar uma reta, precisamos encontrar dois pontos.
Vamos considerar :
Então o ponto pertence ao gráfico.
Agora vamos considerar :
Então o ponto também faz parte do gráfico.
Temos o suficiente para desenhar o gráfico!
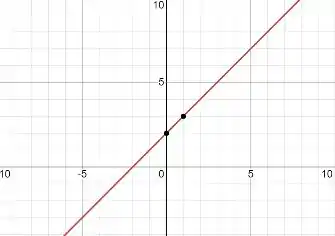
Opa, opaaa! Temos aqui um aluno topíssimo que conseguiu vencer mais uma questãooo!
Bora aproveitar esse embalo e resolver mais? Hehehehe
Resposta
