UTFPR, Sem Campus, Cálculo Diferencial e Integral 1, Profª Lilian Brambila - Lista 2, Questão 4j
Com base no domínio, contradomínio e imagem encontrado no exercício 1, faça o esboço das funções abaixo. Para a funções trigonométricas também exiba o período da função
Passo 1
Eaew, belezinha?
O enunciado nos pede para com base no domínio, contradomínio e imagem encontrado no exercício 1, fazer o esboço da função e também exibir seu período
Então vamos lá!
Passo 2
Primeiro vamos encontrar o domínio, olhando para a função
não temos restrições no argumento da função seno, desde que , temos então que o domínio de é:
Agora vamos encontrar o contradomínio da função. Temos que o contradomínio são os reais:
.
Agora vamos encontrar a imagem da função. Como se trata de uma função seno os resultados serão limitados entre -1 e 1,
Assim, a imagem será:
Passo 3
Para encontrar o período temos que:
O período da função seno é , então
Passo 4
Conhecendo essas informações, construímos o esboço da função e mostramos que :
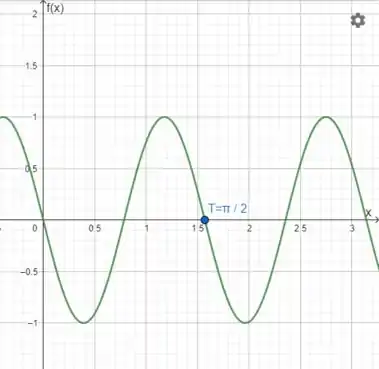
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
No decorrer da questão.