UFCG, Sem Campus, Cálculo Diferencial e Integral III, Listas - Profª Pamella Queiroz - Lista 1 - 2022.1, Questão 1.1ef
Em cada caso identifique e represente graficamente o domínio da função .
Passo 1
Oiie, tudo bem?
O enunciado nos dá duas funções, sendo elas
e, precisamos determinar o domínio destas funções! Isso significa, analisar as funções para obter limitações nos valores de , o caminho costuma sempre ser analisar expressões algébricas que surgem devido a restrições dadas pelo formato da função! Vamos começar com a primeira alternativa! Vem comigo!
Passo 2
Temos que determinar o domínio da função
Temos duas limitações que devem ser consideradas! Primeiro, não existe logaritmo de números negativos, portanto
Além disso, não podemos ter números negativos dentro da raiz, como logaritmo de um número menor que é negativo, portanto, temos que
Ou seja, os valores na seguinte circunferência não pertencem ao domínio
ou, em notação de conjuntos, temos que
que pode ser representado no plano como
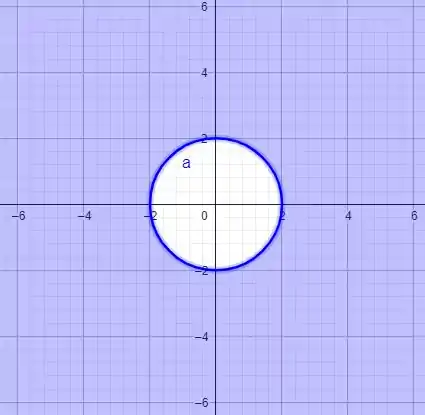
Vamos fazer a outra agora! Bora lá!
Passo 3
Temos a função
Dentro do logaritmo n��o podemos ter valores negativos, pois o logaritmo não estaria bem definido! Portanto
a variável não tem nenhuma limitação! Portanto, o domínio é simplesmente
Vamos representar no plano! Temos que
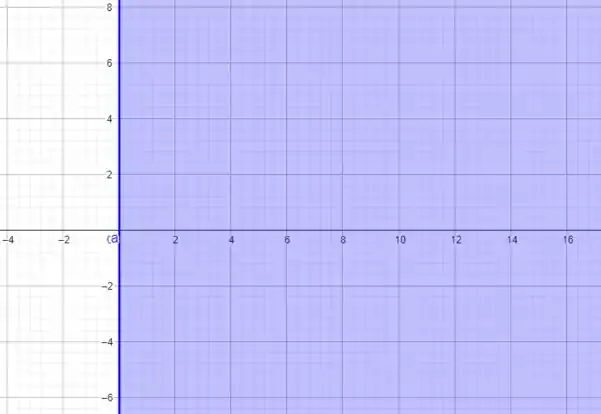
A questão é isso! Te vejo na próxima! Tchauzinho!