1.1. Para cada função dada, determine o domínio e faça um esboço dele:
f)
Passo 1
Iae! Como vai, meu querido? 😁 Bora aprender mais uma questão? 😉

Nesse problema queremos obter o domínio da função e obter um esboço do seu gráfico.
Parece tranquilo? 👀
Para obter o domínio de uma função, temos que analisar a função em si e se perguntar quais os possíveis valores as variáveis podem admitir para que a função seja definida no espaço real.
Legal, né? 😊
Já para obter o gráfico da função, podemos usar algumas arte manhas, como por exemplo obter algumas curvas de níveis da função fazendo e definindo algum valor para onde seja definido, ou também fixar alguma das variáveis a um constante e esboçar seu gráfico em duas dimensões no plano onde a variável foi fixada.
Entendeu? Bora lá! 😉
Passo 2
Vamos começar analisando a função .
Vemos que a função se trata de uma função logarítmica e com base nas características da função sabemos que esta só é definida se , ou seja, se o conteúdo dentro do for maior que .
Trazendo isso para o nosso problema, temos que
Desenvolvendo essa inequação, vamos chegar em
Reescrevendo isso no domínio, vamos obter
Tudo certo? 😉
Passo 3
Agora vamos tentar esboçar o gráfico de
Aqui vamos usar o método dos níveis fazendo
Elevando os dois lados por ...
Assim para , temos
Para
Para
Esboçando essas curvas no plano
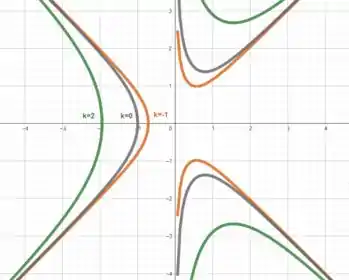
Quanto mais curvas esboçarmos mais fácil é visualizar como a função se comporta. Assim, podemos imaginar como a função se comporta
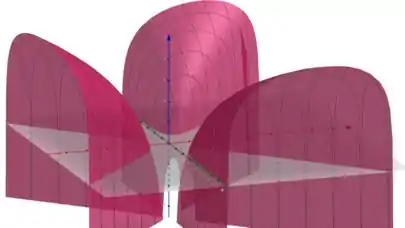
Pegou o esquema? Responde Aí! 😁