UFU, Sem Campus, Cálculo 1, Prof° Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 3.13b
Considere a função cujo gráfico é dado a seguir e faça o que se pede
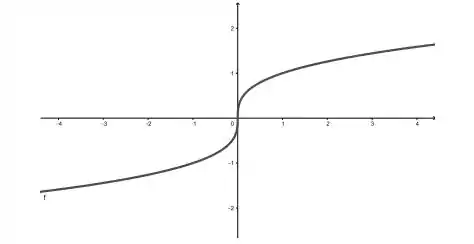
Determine o domínio e a imagem da função inversa de ;
Passo 1
Eaew, belezinha?
A questão nos dá o seguinte gráfico de uma função
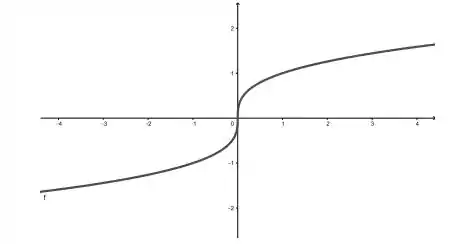
e, esta alternativa pede para determinarmos o domínio e a imagem de uma inversa , para isso, vamos lembrar que para uma função
em que é o domínio e o contradomínio da função, a inversa existe de forma que
Consegue identificar o que isso quer dizer? Vem comigo!
Passo 2
O domínio de nossa função é claramente os reais, note que traçando uma linha vertical sobre qualquer valor de no gráfico a seguir
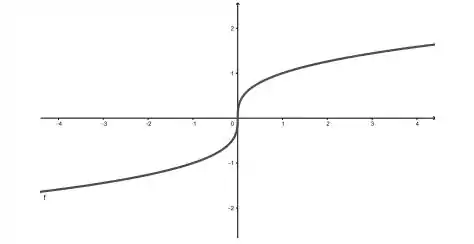
a reta sempre irá cruzar a curva uma vez! Portanto,
isso nos garante que o contradomínio de nossa inversa é dado por
Antes de fazermos afirmações sobre a imagem, vamos analisar o domínio de nossa inversa! Belezinha?
Passo 3
O gráfico da função aparenta ter duas assíntotas horizontais em e , isso limitaria o contradomínio de no intervalo
Isso faz com que o domínio de nossa inversa seja dado por
Se neste intervalo tivermos que o gráfico de nossa função percorre todo o eixo , então o nosso contradomínio é igual a imagem . Como, por definição temos que admite inversa, então ela é bijetora, temos que também deve ser bijetora e portanto, sobrejetora, garantindo que o contradomínio é igual a imagem! Temos então que
A alternativa foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
e