- Dada a função definida por
- Trace o gráfico de e determine o e
- Discuta a continuidade de nos números , e .
Passo 1
Fala aí! Tudo certinho com você? Bora comigo resolver essa questão aqui pra começar a esquentar nossos estudos?
E a primeira coisa que temos que fazer é entender o que a questão está querendo que a gente faça. Ela diz que existe uma função , e joga isso aqui no nosso colo:

Eu sei que é esquisita, mas calma. Essa aí é uma função dada por partes. Repara só nas condições de cada linha, elas dizem pra gente que no intervalo descrito, a função terá um comportamento específico. Por exemplo, na primeira linha temos
Mas a condição diz que isso só é válido para valores de . Sacou?
Já na segunda linha, temos outra regra para outro intervalo, e assim por diante.
Na letra a) no problema teremos que traçar o gráfico de e determine o , que é o domínio da função e que é a sua imagem.
Já no item b) vamos discutir a continuidade da função nos números , e .
Vamos então nos preocupar primeiro em desenhar o gráfico da função, assim vamos conseguir as outras respostas analisando o gráfico construído. Beleza?
Vem comigo que eu vou te ajudar com isso!
Passo 2
Vamos nos concentrar em desenhar o gráfico na nossa função. E como ela é dada por partes, nós já podemos separar nosso plano cartesiano de acordo com os intervalos de cada parte. Veja:
Cada cor representa um intervalo, então agora basta olharmos a cara da função em cada um deles, ok?!
Nossa função é essa aqui:
E o primeiro intervalo é para valores de , onde a função assume a forma de
Ou seja, vamos desenhar essa função só na parte azul no plano.
Ahhh, vela que vamos acrescentar uma bolinha fechada no final do gráfico porque o sinal que limita o intervalo é um , isso significa que o obedece a essa lei de formação da função.
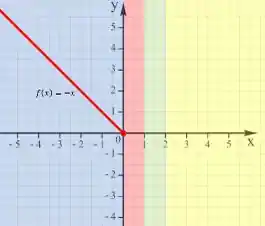
Agora o segundo intervalo é de , e a função assume a forma de
Que é nossa função identidade.
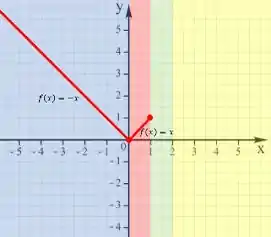
Agora o terceiro intervalo é de , e a função assume a forma de
Aqui o intervalo é aberto, pois , então usaremos uma bolinha aberta no final do gráfico, que fica dessa forma:
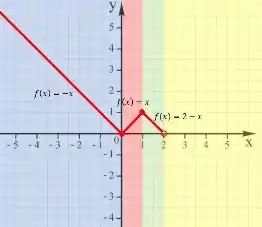
E por fim, vamos desenhar o último intervalo para , em que nossa função será:
E terminamos nosso gráfico da seguinte forma:
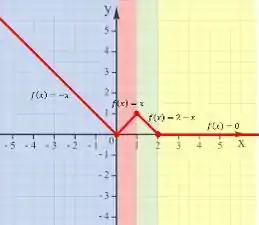
Agora o que nos resta e responder as outras perguntas feitas pelo problema.
Passo 3
Na letra a) também é pedido para que a gente determine o , que é o domínio da função e que é a sua imagem.
Olhando para o gráfico podemos dizer que o domínio da função é todo o conjunto Real, isso porque o domínio são todos os valores de em que a função está definida. Para confirmar isso, você pode pegar qualquer valor de e procurar o valor da função nele que você irá encontrar, logo podemos dizer que:
Já a imagem da função é o conjunto de valores que a função pode assumir, e para isso também podemos olhar para o gráfico e perceber que a função não assume valores menores do que zero. Assim dizemos que:
Maravilha, agora vamos para a letra b)
Passo 4
Na letra b) o problema pede pra gente discutir a continuidade da função nos números , e , e nós também podemos fazer isso olhando para o gráfico que desenhamos. Isso porque podemos dizer que uma função é contina quando seu gráfico não apresenta nenhum salto ou buraco, e é isso que acontece com o gráfico da nossa função. A linha vermelha que o representa é toda contínua.
Assim, dizemos que a função é contínua em todo intervalo real incluindo os números , e .
E depois de tudo isso, fechamos nosso problema.
Partiu pro próximo!!!
Resposta
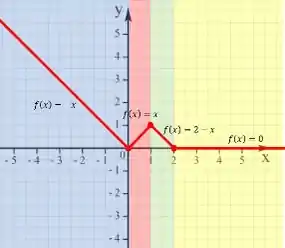
b) Analisando o gráfico vemos que a função é contínua em todo intervalo real incluindo os números , e .