UFSCar; Cálculo I – 1ª Lista de exercícios - Revisão de funções – Ex. 2f
2) Determine o domínio e esboce o gráfico das funções
f)
Passo 1
Oi pessoal, como vão?? Me contaram aqui que vocês estão suuuper animados com essa resolução, felizes pra caramba, como nunca estiveram!!
Não quero saber de desânimo!! Bora transformar ela em algo legal e mais atrativo? hahahaha a gente consegue, acreditem!! Bora lá!!
Bem, para entendermos o que é um domínio, precisamos definir o que é função. Conhecemos como função uma relação entre dois conjuntos A e B em que, para todo elemento do conjunto A, existe um único correspondente no conjunto B. A “ferramenta” que transforma os elementos do conjunto A em um elemento do conjunto B é o que chamamos de função.
Assim já definimos quem é o domínio. O domínio é o conjunto numérico formado pelos valores que pode assumir na nossa função.
Já para a construção do gráfico, usaremos métodos específicos para cada função, levando em consideração algumas simplificações possíveis e características do grau e forma da função.
Muito legal, não é? Então bora calcular!
Passo 2
Como vimos no Passo 1, o domínio é formado pelos possíveis valores de . Aqui procuramos se há algum valor de que torna a função impossível de ser resolvida.
Não há nenhuma restrição para os valores de que torna a função impossível de ser calculada. Como a função está em um módulo, qualquer valor de servirá. Então o domínio da função são todos os números reais:
Passo 3
Agora, para o gráfico, vamos começar identificando qual é o tipo dessa função.
Essa é uma função modular, já que possui um módulo como variável. Não há uma maneira melhor de encontrar o gráfico dessa função do que supor valores para e verificar qual o seu resultado. Vamos colocar alguns valores negativos, o e alguns valores positivos.
Para :
Então o ponto faz parte do gráfico.
Para :
Então o ponto faz parte do gráfico.
Para :
Então o ponto faz parte do gráfico.
Para :
Então o ponto faz parte do gráfico.
Para :
Então o ponto faz parte do gráfico.
Agora podemos montar o gráfico!
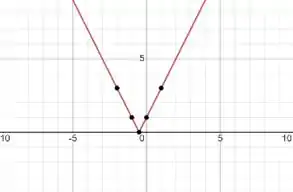
Pra essa questão é isso, pessoal! Mais fácil do que você imaginou, fala aí!
Vamos juntos resolver mais uma?
Resposta
