1.3) Determine e esboce o domínio da função
a)
b)
Passo 1
Falaaa... beleza??? Nessa questão vamos achar o domínio e depois esboçá-lo.
Pra achar o domínio vamos garantir algumas coisas na função:
- se for fração, não pode ter denominador igual a 0;
- se for uma raiz quadrada, dentro só pode ter valores positivos ou igual a zero;
- se for um logaritmo, o que tem dentro dele é estritamente positivo.
E daí podemos esboçar.
Passo 2
Aqui nós temos duas situações, então vamos ter que juntar duas condições.
Temos a raiz, que os valores dentro ou são positivos ou igual a zero:
E também temos a fração, que o denominador não pode ser igual a zero:
Então vamos ter o domínio:
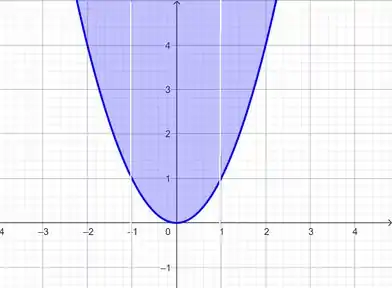
Esboçando: