Encontre o domínio da função
Passo 1
Oi pessoal, tudo bem? Vamos começar?
O problema começa nos dando uma função
e pediu para encontrar o domínio dela. Mas você lembra como encontrar?

O domínio de uma função é o conjunto de todas as entradas possíveis de . Em outras palavras: vamos precisar investigar onde essa função não funciona e retirar esses pontos do conjunto dos reais (nosso maior conjunto possível)
Precisamos fugir de:
- Divisão por zero
- Raíz de índice par de número negativo
- Logaritmo de número menor do que
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Nossa função tem uma raiz de índice par no denominador
Então precisamos garantir que dentro da raiz não tenha número negativo e que o denominador seja diferente de zero!
 Beleza?
Beleza?
Assim temos
Olhando o gráfico das raízes temos
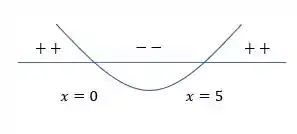
Isso acontece quando
Ou
Assim o domínio
Beleza? Espero ter ajudado!
Até a próxima!