UERJ, Sem Campus, Cálculo I, Listas de Cálculo 1 - UERJ - Lista 1, Questão 3c
Encontre o domínio da função:
c)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar o domínio da função . Pra determinar o domínio de uma função a gente sempre precisa pensar nos valores que pode ou não assumir. Isso porque o domínio é o conjunto de todos os valores possíveis para a variável independente da função.
Nos casos em que a função não possui nenhuma restrição no domínio, seu domínio é o conjunto dos números reais. Mas nem sempre vai ser o conjunto completo, porque tem alguns valores que a função não pode assumir.
No nosso caso, temos uma fração, que não pode ter denominador igual a zero, e uma raiz de índice par, que não pode ter negativo. Essas vão ser nossas restrições.
Vamos lá!
Passo 2
Como nosso denominador não pode ser zero e não pode ser negativo (maior ou igual a zero), temos para :
Podemos colocar em evidência:
Para que um produto entre dois números seja positivo (maior do que zero), os dois precisam ter sinais iguais, ambos negativos ou ambos positivos. Vamos analisar, então, os casos:
E
Passo 3
Para o caso em que ambos são positivos, e , temos na reta numérica:
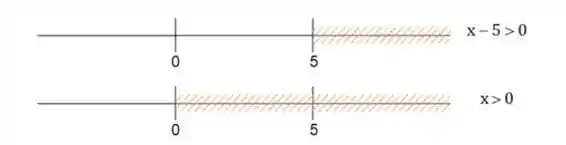
Podemos ver que possui parte de , então a interseção dos dois conjuntos nos dá:
Agora para o caso em que os dois termos são negativos, e , temos:
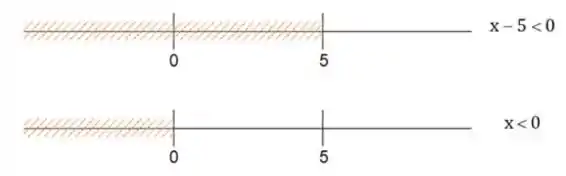
Também dá pra ver que possui parte de , então temos que:
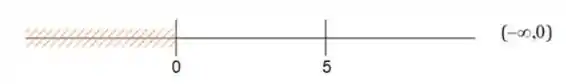
Então, nosso domínio vai ser a união dos dois conjuntos resultantes para os dois casos, ou seja:
Prontinho, galera! Até a próxima! 😉