Encontre o domínio da função . Encontre as coordenadas dos pontos em que o gráfico da função corta os eixos coordenados.
Esboce o gráfico de . Explique a construção do gráfico da função ,
usando transformações em gráfico (translações, reflexões...) a partir do gráfico da função .
Descreva essas transformações em palavras.
Passo 1
Eaee!!! Belezinha? Bom... queremos encontrar o domínio da função , as coordenadas dos pontos em que o gráfico da função corta os eixos coordenados e esboçar o gráfico e explicar a construção do gráfico.
Passo 2
Bom... seja , temos que seu domínio é:
Assim, temos:
- Para :
- Para :
O que é impossível!
Logo, o único ponto de contato com o eixo das coordenadas é
Passo 3
Agora, esboçando , temos:
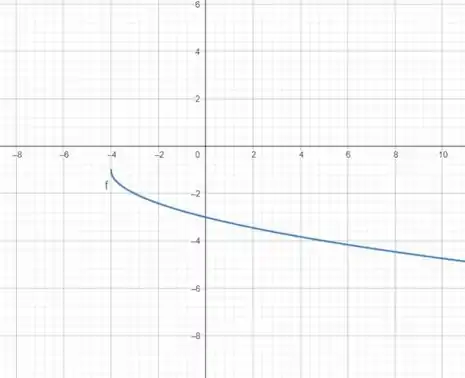
Esse gráfico também pode ser obtido fazendo as seguintes manipulações no gráfico :
- Translação em uma unidade para baixo;
- Translação em 4 unidades para esquerda;
- Reflexão no eixo .
Entendeu direitinho? Responde aee ;)

Resposta
No texto