UFMG, Sem Campus, Cálculo 3, P1 – 2023.1 – Questão 2
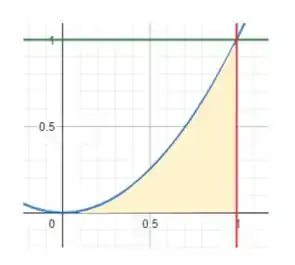
Esboce a região da integração e mude a ordem de integração para calcular a integral:
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá.
Vamos pegar a integral do enunciado:
Para esboçarmos, precisamos antes determinar o intervalo de variação de . Olhando para a integral acima, vamos reparar que o primeiro intervalo vai ser referente ao e o segundo intervalo vai ser referente ao
Show. Agora, vamos começar a desenhar com calma cada parte. Começando pelo intervalo de
Temos que
Então, vamos ter algo parecido com isso:
Agora em relação a . Antes, vamos fazer um pequeno ajuste. Repara que temos
Para ficar mais simples de desenhar, vamos re-escrever o
Show, desenhando, vamos ter:
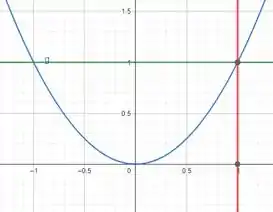
Passo 2
Show, agora vamos mudar a ordem de integração da nossa integral:
Reparem que aqui temos uma integral dupla do tipo , ou seja, está entre números e está entre funções. O que faremos aqui? Vamos inverter isso. Primeiro temos que extrair os intervalos de integração que fizemos lá no Passo 1:
Para isso vamos dar uma conferida na região delimitada:
Agora vamos trazer de volta a nossa região encontrada no Passo anterior:
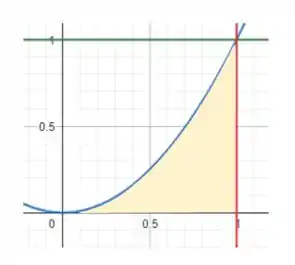
Reparem que o Intervalo de integração da nossa região está como se tivesse indo da Esquerda para a Direita, por isso está entre funções. Então, vamos ter que agora olhar para ela indo de baixo para cima, e assim colocar entre funções.
Começando por . Reparem que pela nossa imagem, está variando de . Logo:
Show, agora, olhando para . Reparem que nós vamos ter a curva em Azul acima do nosso eixo . Mas afinal, que curva é essa? Bom, nós calculamos lá no Passo 1:
Podemos isolar o :
Então podemos dizer que esta variando entre :
Com isso, nossa integral dupla vai ficar:
Resposta
