UFRJ – Cálculo 2 – 2020.2 - Testes – P2 – Questão 1
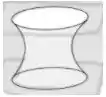
Qual figura melhor esboça o maior domínio de definição da função
Passo 1
Fala galera, beleza? Bora resolver o nosso exercício? Vamos lá.
Para a gente entender o domínio da função, temos que analisar com calma cada restrição que pode ter ali. Vamos começar olhando para a função logaritmo.
Os valores dentro da função logaritmo tem que ser maiores que zero, então
Passo 2
Show galera, agora vamos analisar a equação dentro da raiz. Quando temos uma raiz, ela tem que ser maior ou igual a zero, então
Beleza, porém aqui nós vamos ter que fazer um preenchimento de quadrados na parte da variável y
Se a gente isolar o 2 na parte do y, vamos ter:
Para a gente deixar a nossa equação mais próxima do formato padrão, vamos deixar no numerador somente as variáveis ao quadrado
Passo 3
Beleza, então, o que podemos concluir com isso? Vamos olhar para a última fórmula encontrada
Essa fórmula se trata de uma Hiperbolóide de uma folha. Porém ele ta dizendo que tem que ser maior do que 1, logo a região seria a parte de FORA da hiperbolóide.
Além disso, nós temos mais 1 restrição:
Ou seja, a altura da nossa hiperbolóide vai variar de -2 até +2, então tem uma região limitada.
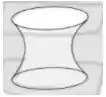
Resposta
