UFF, Niterói - Campus da Praia Vermelha, Cálculo IA, Provas de C1 - Profº Leonardo - VE1 - 2023.1, Questão 1d
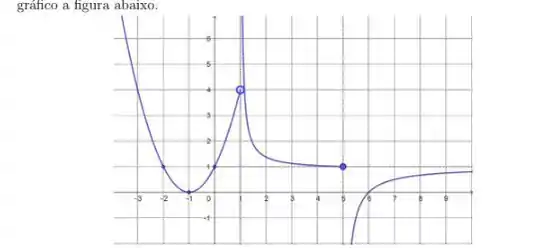
Uma função com domínio tem como gráfico a figura abaixo.
Passo 1
Para determinar o domínio da função composta , precisamos considerar os valores de que garantem que as composições de sejam válidas.
O domínio da função será dado pela interseção dos domínios de e . Vamos analisar cada um deles separadamente:
Passo 2
Domínio de :O domínio de é , ou seja, todos os valores reais exceto .
Domínio de :O domínio de é determinado pelos valores de para os quais é definida. Isso significa que o valor deve estar dentro do domínio de , que é , exceto . Isso implica que deve ser um valor real, exceto .
Portanto, o domínio de será a interseção dos domínios de e , que é , exceto .
Resposta
Domínio de , ou seja, todos os valores reais exceto .
Exercícios de Livros Relacionados
Verificar quais das seguintes curvas são suaves:a) r → t = t 3 i → + t 2 j → , t ∈ - 1,1
Verificar que as equações vetoriais r → w = w ,w 2 ,2 ≤ w ≤ 3 e r → t = t ,t , 4 ≤ t ≤ 9 representam a mesma curva.
Verificar quais das seguintes curvas são suaves:e) r → t = 2 cos t ,3 s e n t , t ∈ 0 ,2 π
Verificar quais das seguintes curvas são suaves:d) r → t = 3 cos 3 t ,3 s e n 3 t , t ∈ π 6 , π 3
Verificar quais das seguintes curvas são suaves:b) r → t = t 3 i → + t 2 j → , t ∈ 1 2 , 1