USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 1, Questão 7.39
Um papel de filtro circular de raio a deve ser transformado em um filtro cônico cortando um
setor circular e juntando as arestas CA e CB (veja a Figura 3a). Ache a razão entre o raio e a
profundidade do filtro de capacidade máxima.
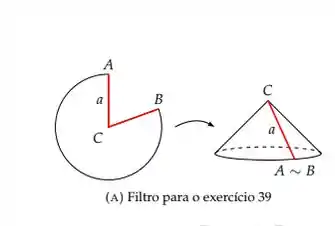
Passo 1
Fala galera, tudo bem com vocês? Vamos para mais uma questão de Cálculo 1.
Queremos descobrir qual a razão entre o raio e a profundidade do filtro de capacidade máxima.
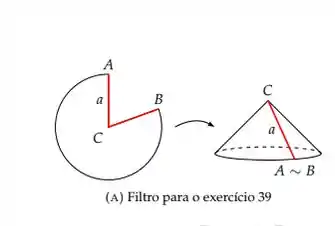
Bem, se estamos falando de capacidade máxima, precisamos calcular o volume do filtro. Para isso precisamos descobrir algumas medidas.
Passo 2
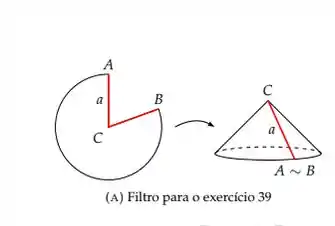
Seja , o menor ângulo . Dessa forma, temos que o comprimento do menor arco é dado por:
Dessa forma, o comprimento da circunferência do nosso cone é nosso cone
Com isso, podemos definir o raio dessa circunferência como:
Vamos chamar , para simplificar a notação:
Agora que temos nosso raio da base do cone. Podemos usar pitágoras para descobrirmos a altura. Temos que:
Logo
Passo 3
Agora que temos o raio e a altura do cone. Podemos calcular seu volume. Que é dado por
Vamos descobrir para qual valor de o volume é máximo, derivando e igualando a zero temos:
Cujas raízes são:
Fazendo o estudo de sinal da primeira derivada. Vemos que o ponto de máximo ocorre em
Passo 4
Logo, a razão entre o raio e a altura do cone de maior volume é:
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊