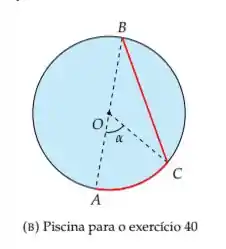
Para ir de um ponto a um ponto diametralmente oposto de uma piscina circular de de diâmetro, uma pessoa pode caminhar (com velocidade constante) pela borda da piscina até um ponto e nadar (com velocidade constante) em linha reta até o ponto (vide Figura 3b). Seja o ângulo . Sabendo que ela pode caminhar duas vezes mais rápido do que pode nadar, determine, em termos de , as trajetórias que o levam ao seu destino no maior e no menor tempo. (Observação: considere que a pessoa pode somente caminhar ou somente nadar).
Passo 1
Fala galera, tudo bem com vocês? Vamos para mais uma questão de Cálculo 1.
Queremos descobrir qual o maior e menor tempo que uma pessoa leva para atravessar uma piscina circular de de diâmetro, onde a pessoa pode caminhar (com velocidade constante) pela borda da piscina até um ponto e nadar (com velocidade constante) em linha reta até o ponto (vide Figura 3b). Seja o ângulo . Sabendo que ela pode caminhar duas vezes mais rápido do que pode nadar.
Vamos supor que a velocidade que a pessoa nada é . Logo, a velocidade com a qual ela anda é
Com isso em mente. Vamos calcular a distância percorrida pela pessoa no trajeto.
Passo 2
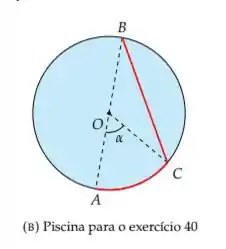
A distância percorrida será o tamanho do arco mais o segmento de reta .
Bem, como a piscina tem raio o comprimento do arco é:
Agora, qual seria o comprimento da semirreta ? Vamos desenhar
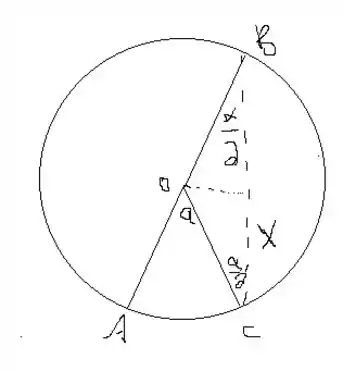
Como o triângulo é isósceles, temos que sua base será dada por
onde
Logo, a distância percorrida a nado é
Passo 3
Agora que temos as distâncias percorridas a pé e a nado. Podemos calcular o tempo que a pessoa leva para percorrer cada uma delas. Como
Temos:
Dessa forma, o tempo total é:
Para obtermos o tempo mínimo, derivamos e igualamos a zero. Derivando
Note que que é zero quando
Agora, só temos um ponto crítico que é o máximo. Logo, o mínimo local se encontrará na fronteira dos valores de por conta do teorema de Weierstrass. Logo mínimo ocorre em
ou
Substituindo os valores, vemos que o mínimo ocorre em:
Dessa forma, temos que:

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊