UFMG – Cálculo 2 – 2022/2 – Lista de exercícios 7
1.1) Seja
a) Calcule e
b) Determine e esboce o domínio de .
c) Determine a imagem de .
Passo 1
Falaaa... Beleza??
Nessa questão vamos usar os conceitos de funções de várias variáveis.
Na letra (a), pra calcular vamos só substituir os valores de e na função e calcular.
Na letra (b), pra achar o domínio vamos garantir algumas coisas na função:
- se for fração, não pode ter denominador igual a 0;
- se for uma raiz quadrada, dentro só pode ter valores positivos ou igual a zero;
- se for um logaritmo, o que tem dentro dele é estritamente positivo.
E daí podemos esboçar.
Na letra (c), pra achar a imagem vamos ver quais são os valores possíveis pra
Passo 2
a) Substituindo os valores:
Passo 3
b) como temos uma função logarítmica, então o que tem dentro dela tem que ser estritamente positivo:
E o domínio fica:
E o esboço fica o plano:
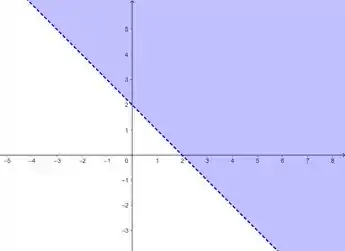
Passo 4
c) Como a função é logarítmica, então todos os números reais fazem parte da imagem.
Se não for tão fácil enxergar isso, lembra da função exponencial, que é a inversa da logarítmica. O domínio da função exponencial é o conjunto de todos os reais, né?? Então a imagem do log será o conjunto dos reais também.
Acabamos essa. Bora pra próxima?
Resposta
a) e
b)
c)