UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 2.9i.
9. Usando o conhecimento do gráfico da função potência , para um inteiro , produtos notáveis e as noções de deslocamento horizontal e vertical, trace um esboço do gráfico das seguintes funções:
(i) .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nessa questão, queremos obter o gráfico de .
Mas nossa função é dada por
Então p que temos que fazer é tentar simplificar essa função aí para conseguirmos obter o gráfico de de uma maneira mais simples.
A função é uma fração polinomial, portanto, podemos fatorar um dos polinômios para simplificar essa fração.
Bora começar! 😁
Passo 2
Se fatorarmos o polinômio de grau , temos
Substituindo em ...
Perceba que aparece multiplicando o numerador e o denominador, logo, podemos simplifica-lo.
Assim, vemos que nossa função pode ser reescrita simplesmente como .
Tranquilo até aqui? 🤔
Passo 3
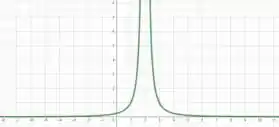
Agora podemos obter o gráfico de analisando alguns aspectos.
Em , não está definido e conforme se aproxima de , tende a já que tende a um número muito pequeno.
Outro aspecto também é que nunca assume valores negativos. Como está elevado ao quadrado, o resultado sempre será um valor positivo.
E também, se for muito grande em módulo, tende a , já que o denominador será muito grande.
Resumindo essas características em um gráfico, temos algo mais ou menos assim
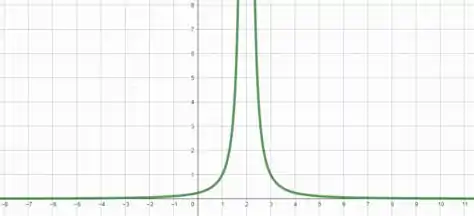
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
