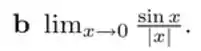
Passo 1
Começamos substituindo esse cara aí:
Indeterminação! Vamos usar algum processo que elimine esse .
Passo 2
Temos que o módulo de é dado da seguinte maneira:
Então, lateralmente, teremos o seguinte:
Vamos calcular os dois limites laterais agora e, se eles convergirem para o mesmo valor, esse será o limite pedido no enunciado.
Passo 3
Assim, calculamos os limites laterais, usando ali o limite fundamental do seno sobre :
Logo,
E se os limites laterais são diferentes...
Resposta
Exercícios de Livros Relacionados
Calcule.underset(x - 0)(lim) x sen (1)/(x)
Calcule.underset(x - 0)(lim) (tg x)/(x)
Calcule.underset(x - p)(lim) (sen (x^2 - p^2))/(x - p)
Calcule.underset(x - p)(lim) (tg (x - p))/(x^2 - p^2) , p != 0
Calcule.underset(x - 0)(lim) (x - tg x)/(x + tg x)