UFSC – Cálculo 1 – Lista 1.10 – Questão C1h
Calcule os limites abaixo
Passo 1
Oi pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Bora lá?
A ideia é calcular esse limite aqui
Nosso instinto é substituir e ver no que dá, não é verdade? Vamos ver o que encontramos:
Uma indeterminação! Ou seja: precisamos manipular esse limite para conseguirmos levantar essa indeterminação!
Mas calma! Antes vamos relembrar de duas coisas: dos limites fundamentais (trigonométricos e envolvendo exponenciais) e de uma identidade trigonométrica (meio obscura) muito útil!
Primeiro a identidade trigonométrica
Beleza?
E, por fim, estão aqui os limites que você precisa ter na manga para resolver qualquer questão assim:
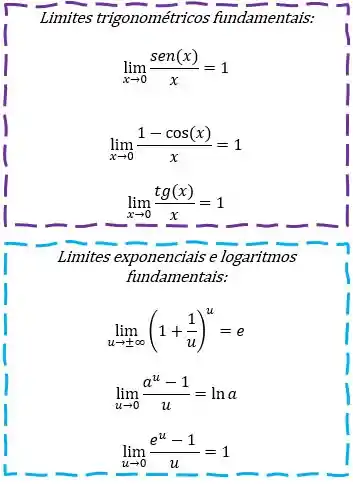
E aí? E depois? Depois é #partiu #manipulação para deixar o nosso limite com a cara de um limite fundamental! Assim vamos conseguir usar os resultados e calcular o nosso limite de boas!
Então a ideia é usar essas informações para calcular o nosso limite!
Mas relaxa!
Vamos fazer passo a passo, juntinhos!
Passo 2
Primeiro vamos olhar para nosso limite
Comecei colocando em evidência! A ideia aqui é usar o terceiro limite fundamental da caixa em azul
Beleza? Agora precisamos arrumar esse denominador... vamos usar a identidade trigonométrica!
No nosso caso :
E bora substituir no nosso limite
Mas melhorou! E eu vou te mostrar! No denominador temos agora e que quando , , já é menos uma indeterminação! E agora? Agora temos um seno embaixo e aquele parênteses em cima, já vamos bem misturar dois limites fundamentais!
Vem comigo!
Passo 3
A ideia agora é #manipulação
Sabemos que o produto dos limites é o limite dos produtos, então olha só, vamos separar tudo que não gera indeterminação:
E aquele segundo limite? Vou te lembrar desses dois limites fundamentais:
O que faltam neles? Um ! Se multiplicarmos e dividirmos por o segundo limite vamos poder combinar esses dois resultados!
E taí nosso resultado!
Beleza?
Espero ter ajudado!