- Calcule os limites abaixo, se existirem.
d.
Passo 1
Oi, galerinha! Tudo bom? Para resolver esse limite, vamos dar uma olhada na definição de limite:
De fato, a definição formal de limites é um pouco complexa, mas vamos iniciar de uma forma mais fácil. Supondo que, a partir do primeiro gráfico, a função não fosse contínua em e tivesse essa forma:
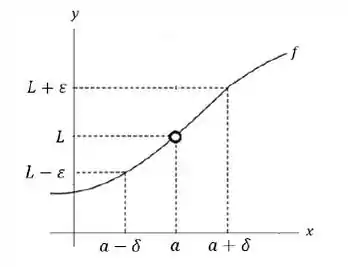
Onde as constantes (épsilon) e (delta) são pequenas variações, para mais ou para menos, dos valores de 𝐿 e 𝑎 respectivamente. Neste caso, vemos que não está definida em 𝑎, mas existe um limite 𝐿 que satisfaça uma condição específica que apresentarei logo adiante.
Ou seja, se para todo número houver um número , tal que se
Então,
Agora vamos olhar para na nossa função!
Passo 2
Aqui nós temos uma função cosseno que é periódica.
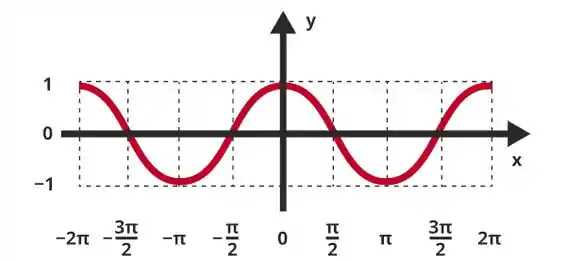
Repara que ela se repete em intervalos de até . Então temos que para existe um número natural , tal que:
E
Teremos também,
E
Então para todo é falsa a afirmação de que existe tal que para todo
Assim,