Calcule, sem usar regra de L’Hôspital, os limites abaixo ou prove que não existe. Justifique suas respostas:
- Seja uma função tal que para todo . Usando o teorema do confronto, calcule o limite (e justifique)
Passo 1
Fala galera bonita, tudo certo? Bom, pra começar, a gente sempre mas seeeempre checa primeiro os limites substituindo o valor proposto. Se não der indeterminação, tamos feitos! Vamos ter:
É pessoal, três indeterminações. Então não tem jeito! Vamos precisar mexer nesses limites até eles ganharem uma forma que suma a indeterminação. Bora lá?
Passo 2
Letra a)
Pra letra a macete vai estar em ver que ela é uma função que tem fração de polinômio e função trigonométrica. Quem tem essa cara também é o limite fundamental trigonométrico! Vamos então tentar fazer surgir:
Pra isso, uma boa ideia, pra fazer o seno aparecer, é multiplicar em cima e em baixo pelo conjugado do numerador:
Ok, mas nós temos um seno ao quadrado ali em cima? Pô, pra casar, vamos deixar um em baixo, multiplicando em baixo e em cima:
Das propriedades dos limites, temos:
Limite fundamental trigonométrico apareceu, aee! Substituindo, temos:
Passo 3
Letra b)
Pra letra b) o truque vai ser olhar pra raiz e pensar: humm, se eu me livrar dela, as coisas ficam mais fáceis, né? Então, uma forma de fazermos isso, é multiplicar pelo conjugado em cima e em baixo:
E olha só que doido! Isso já foi o suficiente! Substituindo , achamos:
Letra c)
Nessa letra, o que temos que fazer é o que faremos sempre que tivermos indeterminação do tipo : Colocar tudo no mesmo denominador. Assim, se a indeterminação não sumir, pelo menos podemos achar uma de outro tipo. Pra isso, usando o produto notável:
Vemos que basta multiplicar em cima e em baixo na fração da esquerda pelo seu conjugado pra eles terem o mesmo denominador:
E substituindo agora, temos:
O limite, portanto, não existe! A gente sempre diz que não existe quando:
- Ele é incalculável, como por exemplo
- Ele é calculável, porém resulta em
Passo 4
Letra d)
Pra gente fechar com chave de ouro, bora fazer a letra . Ela nos dá:
Um bom primeiro passo então será isolar na equação. Pra isso, somamos em cada parte dela:
Aplicando o limite, temos:
E veja só, se o limite está entre e , ele só pode ser . É como se tivéssemos três funções
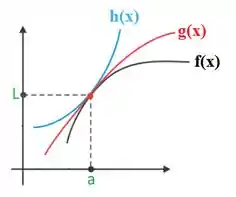
Onde
Se está sempre entre esses dois carinhas e eles tem um limite em comum pra , pra esse mesmo o limite de também dará . Afinal, não tem muito pra onde fugir já que ele tem que ficar preso ali entre !
Resposta
Justificativas no decorrer da resolução
Respostas: