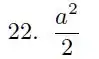Calcule o limite, caso exista. Caso não exista, justifique.
Passo 1
A primeira coisa que devemos fazer ao achar um limite é substituir o valor do ponto na função
Então, temos uma indeterminação e precisamos mexer um pouco no limite.
Passo 2
Sempre que você ver um seno ou cosseno sobre um , e afins, desconfia do limite fundamental trigonométrico! Aquele que diz que
Pô, mas ali não tem seno nenhum! O que vamos fazer é multiplicar em cima e embaixo por e usar a relação fundamental da trigonometria. Vem comigo:
Passo 3
Legal o seno acabou de aparecer. Mas se liga que ali ele está ao quadrado e no limite fundamental não tem nada ao quadrado! Olha a malandragem que eu vou fazer
O limite mais a direita é tranquilo de resolver. Basta substituir 0 na expressão:
Passo 4
O da esquerda tá quase pronto pro limite fundamental! Tá vendo que dentro do seno tem e no denominador só está ? Precisamos multiplicar em cima e embaixo por , para ficar igualzinho!
Agora sim temos o limite fundamental trigonométrico, então teremos que
Passo 5
Juntando tudo, temos que:
Resposta