Avalie os limites abaixo e encontre o correspondente valor caso exista. Justifique suas respostas.
Passo 1
(b) Então pessoal, agora queremos resolver esse aqui:
Aqui também não dá pra substituir direto, porque ia aparecer um zero no denominador.
Mas aquele módulo ali no numerador é muito suspeito! Esse módulo denuncia que o sinal (positivo ou negativo) pode ser relevante nesse limite.
Outra coisa relevante, é que esse limite se parece muito com esse resultado importante:
Que é o limite trigonométrico fundamental. Você pode usar esse resultado já pronto pra demonstrar outros limites sem problema nenhuma.
Passo 2
Então vamos lá, o que acontece quando o se aproxima de zero pela direita, ou seja, por valores positivos? Bom, lembra da definição do módulo?
Então, quando o é positivo (), a gente pode escrever o limite assim:
Porque a função seno é positiva quando se aproxima do zero por valores positivos então o módulo nem vai fazer diferença! Se isso estiver confuso é só ver esse gráfico aqui:
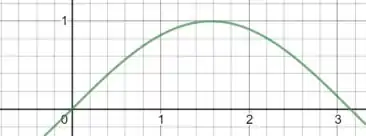
Viu? Quando estamos chegando no zero pela direita, o seno sempre fica positivo perto do zero.
E quando a gente se aproxima por valores negativos (), ou seja, pela esquerda? Bom, o seno é negativo quando se aproxima de zero pela esquerda, então pela definição do módulo:
Beleza, já tiramos o módulo:
Passo 3
Agora vamos dar uma olhada nessa expressão que sobrou. Essa é a hora de aproveitar aquele limite trigonométrico fundamental:
Começando pelo caso (vamos chamar de ). Primeiro vamos colocar aquele expoente do lado de fora da fração:
Ok, estamos quase fazendo o limite fundamental aparecer. Vamos substituir , que também tende a zero pela direita quando tende à zero pela direita:
Tirando aquela constante (:
Agora é só usar essa propriedade dos limites pra tirar o expoente:
Então:
Aquele limite no parênteses é o limite trigonométrico fundamental, que a gente sabe que vale , então:
E o que acontece com o ? É exatamente a mesma coisa, mas com o sinal trocado.
Fazendo a mesma substituição de antes:
Passo 4
Então tá, olha o que a gente descobriu:
O limite pela direita é diferente do limite pela esquerda! Isso quer dizer que o limite não existe!
Então a resposta da letra (b) é essa: o limite não existe, ou então, o limite diverge. Dá uma olhada no gráfico:
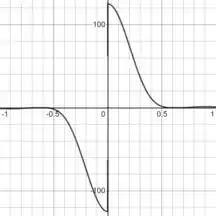
Resposta
(b) O limite diverge. e .