UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista 2 de Exercícios, Questão 31c
Calcule os seguintes limites:
c)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado pediu pra gente calcular o valor da função quando o valor de vai pra mais infinito, ou seja, quando ele tende a valores infinitamente grandes e positivos.
Repare que apenas substituindo zero no lugar de , nós teríamos uma indeterminação, porque nossa denominador zeraria. Então, vamos manipular um pouquinho nossa função pra sair da indeterminação e conseguir avaliar o limite.
Vamos lá!
Passo 2
Temos:
A gente pode separar esse limite assim:
Agora vamos analisar cada limite. Repare que quando tende a valores muito grandes, nossa fração no denominador se aproxima muito de zero, e qualquer número elevado a zero é igual a . Então, temos:
E o arco tangente? Vamos dar uma olhadinha no gráfico dessa função pra perceber o que acontece:
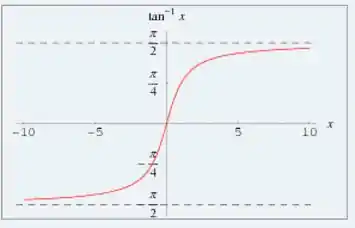
Repare que quando a nossa curva vai pra infinito do lado direito, ela se aproxima cada vez mais de . Portanto,
Assim, nosso limite original vai ficar assim:
Prontinho, galera. Até a próxima! 😉