Listas de Cálculo 1 - Profº Ricardo Martins de Cálculo 1 da UNICAMP - Lista sobre Limites e Continuidade

Estude se as funções abaixo tem limite nos pontos indicados.

, ponto .

Estude se as funções abaixo tem limite nos pontos indicados.

, ponto .

Existe o limite da função dada por

quando ?

Considere a função

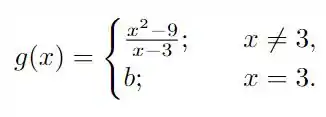
esta função tem limite em ? Qual deve ser o valor de para que a função seja contínua?

Qual a inclinação da reta tangente ao gráfico de no ponto ?

A função é contínua em todos os seus pontos (prove!).

Calcule os limites laterais de no ponto .

Estude, por e , o limite de no ponto .

Prove por e que se então .

Prove que se então .

Calcule os limites abaixo:

Calcule os limites abaixo:

Calcule os limites abaixo:

Calcule os limites abaixo:

Calcule os limites abaixo:

Mostre que é contínua para todo .

Mostre que a função

é contínua na origem.

Estude a continuidade da função

O que acontece quando

Mostre que a função abaixo não é contínua na origem (tente procurar um e veja o que acontece)

Seja . Mostre que essa sequência é crescente e limitada (por exemplo, pelo ).

Mostre que .

Mostre que .

Mostre que não converge.

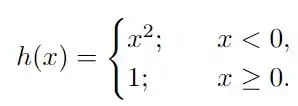
Determine, se existirem, valores de para os quais a função abaixo seja contínua:

Calcule

.

Determine os valores de para os quais existe o limite

.

A função possui assíntotas?

Dê exemplos de funções com assíntotas (dois exemplos para cada tipo).

Calcule os limites abaixo:

a)

Calcule os limites abaixo:

b)

Calcule os limites abaixo:

c)

Calcule os limites abaixo:

d)

Calcule os limites abaixo:

e)

Calcule o que se pede:

a)

Calcule o que se pede:

b)

Calcule o que se pede:

c)

Calcule o que se pede:

d)

Calcule o que se pede:

e)

Calcule o que se pede:

f)

Calcule o que se pede:

g)

Calcule o que se pede:

h)

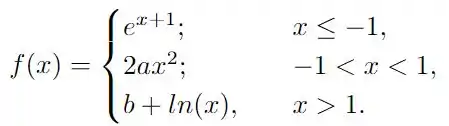
Seja uma função e suponha que para todo , . Calcule . A função é contínua na origem?

Sejam , : com e para todo , fixado. Mostre que .

Calcule .

O limite existe?

O limite existe?

Mostre que a equação tem pelo menos uma solução real.

Mostre que a equação tem pelo menos três soluções reais.

Seja . Existe pertencente a tal que ?

Seja contínua, com e para todo . Mostre que para todo .

Mostre que o conjunto

admite um maior e um menor elemento. Você consegue calcular estes valores?

Calcule os limites abaixo:

a)

Calcule os limites abaixo:

b)

Calcule os limites abaixo:

c)

Calcule os limites abaixo:

a)

Calcule os limites abaixo:

b)

Seja

a) A função é contínua em ?

Seja

b) Existe ?

Qual a semelhança entre o gráfico de

E o pato?

Estude as assíntotas de .

Estude as assíntotas de e esboce seu gráfico.

Resolva e ilustre a solução.

Calcule .

Calcule .

Calcule .

Seja uma função tal que para todo temos

Calcule . Mostre que se for contínua então .

Use o TVI para mostrar que a equação

possui pelo menos duas soluções. Estime estas soluções com casas decimais.

Calcule as assíntotas verticais e horizontais de

Determina para que a função

seja contínua.

Seja

Determine o domínio de e escreva a expressão da função sem usar módulo. Verifique se a função é par ou ímpar, ou injetora. Justifique sua resposta provando ou dando contra-exemplo.

Seja

Encontre todos tais que

Calcule os limites abaixo (sem usar L’Hopital).

Calcule os limites abaixo (sem usar L’Hopital).

Calcule os limites abaixo (sem usar L’Hopital).

Dê condições suficientes e necessárias sobre e para que a função

seja contínua.

Faça o que se pede:

Use o Teorema do Valor Intermediário (TVI) para mostrar que a equação

Possui ao menos uma solução não-nula.

Determine, caso existam, as assíntotas horizontais e verticais de

Calcule os limites abaixo (sem usar a Regra de L’Hospital)

Onde

Seja

1. Existe algum valor de que torna é contínua em ? Justifique sua resposta

Seja

b) Encontre a assíntota horizontal de quando . Existe assíntota vertical em algum ponto?

Use o Teorema do Valor Intermediário para mostrar que a equação

Tem pelo menos uma raiz no intervalo

Encontre o ponto do gráfico de onde a reta tangente é paralela à reta

Determine todos os valores de tais que

Discuta de modo argumentativo a existência ou inexistência de cada um dos limites abaixo, determinando-o quando este existir:

Discuta de modo argumentativo a existência ou inexistência de cada um dos limites abaixo, determinando-o quando este existir:

A função é contínua em ? Justifique sua resposta.

Encontre a assíntota horizontal de quando. Existe assíntota vertical em algum ponto?

Use o Teorema do Valor Intermediário (TVI) para mostrar que a equaç ao

tem uma solução no intervalo

Sejam

(a) Determine os valores de tais que .

Sejam

(b) Faça um esboço do gráfico de .

Calcule o limite abaixo

Calcule o limite abaixo

Calcule o limite abaixo

Calcule o limite abaixo

onde

Determine, se possível, os valores das constantes para que a função

Seja a função

Determine o domínio e imagem de , bem como as ass ́ıntotas horizontais e verticais

do gráfico de (se existirem).

Seja a função

Use o Teorema do Valor Intermediário para mostrar que a equação admite

ao menos três soluções reais.

Seja a função

Um aluno calculou , percebeu que esses números têm sinais

contrários e concluiu que deve existir tal que . Você

concorda com ele? Justifique.

Calcule o limite

Calcule o limite

4.6. A função

é contínua em apenas dois pontos.

4.7. Em quais pontos a função

é contínua?

Calcule o limite abaixo