Listas de Cálculo 1 - USP de Cálculo 1 da USP - Lista 2

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Calcule, caso exista

Seja um polinômio de grau 3, com três raízes reais distintas. Mostre que tem um ponto de inflexão, que é a média aritmética das três raízes.

Seja . O ponto é ponto de

a. maximo local mas nao global.

b. minimo local mas nao global.

c. maximo global.

d. minimo global.

e. inflexao.

Seja uma função cuja derivada tem o gráfico esboçado na figura abaixo

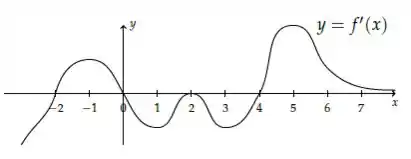
1. Em que intervalos é crescente ou decrescente?

Seja uma função cuja derivada tem o gráfico esboçado na figura abaixo

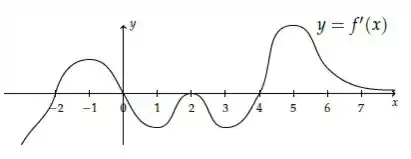
1. Para que valores tem um máximo ou mínimo local?

Seja uma função cuja derivada tem o gráfico esboçado na figura abaixo

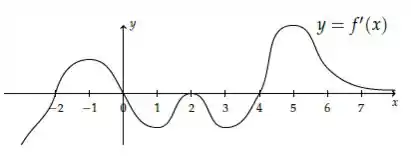
1. Em que intervalos tem concavidade para cima ou para baixo?

Seja uma função cuja derivada tem o gráfico esboçado na figura abaixo

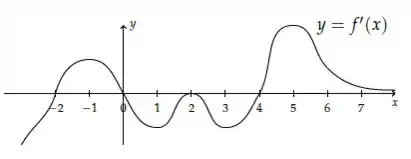
1. Ache os pontos de inflexão de

Seja uma função cuja derivada tem o gráfico esboçado na figura abaixo

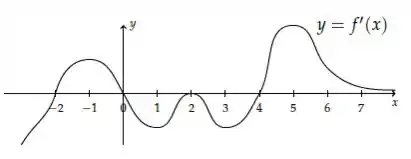
1. Admitindo que , faça um esboço do possível gráfico de

Considere as funções deriváveis e cujos gráficos estão esboçados abaixo:

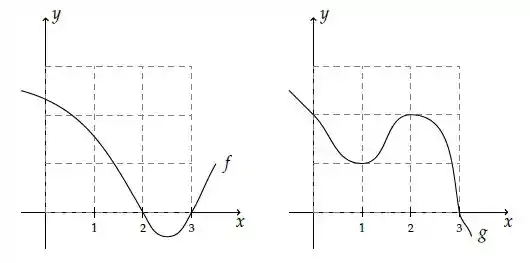
Seja . Sabendo que é ponto de mínimo local de e que , é correto afirmar que

3. é ponto de inflexão de
4. é ponto de mínimo local de
5. é ponto de máximo local de

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Parte 1: determine os pontos de máximos, mínimos, inflexão, bem como os intervalos das concavidades

Parte 2: determine as assíntotas (quando existirem) e o esboço do gráfico.

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Parte 1: determine os pontos de máximos, mínimos, inflexão, bem como os intervalos das concavidades

Parte 2: determine as assíntotas (quando existirem) e o esboço do gráfico.

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Parte 1: determine os pontos de máximos, mínimos, inflexão, bem como os intervalos das concavidades

Parte 2: determine as assíntotas (quando existirem) e o esboço do gráfico.

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Parte 1: determine os pontos de máximos, mínimos, inflexão, bem como os intervalos das concavidades

Parte 2: determine as assíntotas (quando existirem) e o esboço do gráfico.

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Parte 1: determine os pontos de máximos, mínimos, inflexão, bem como os intervalos das concavidades

Parte 2: determine as assíntotas (quando existirem) e o esboço do gráfico.

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Parte 1: determine os pontos de máximos, mínimos, inflexão, bem como os intervalos das concavidades

Parte 2: determine as assíntotas (quando existirem) e o esboço do gr��fico.

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

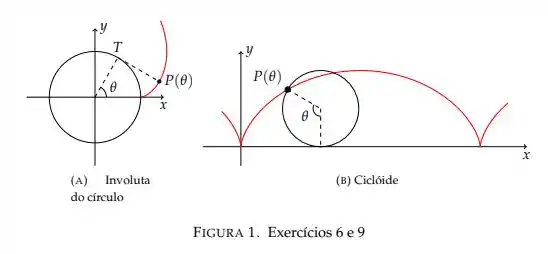
Uma circunferência de raio rola sem escorregar ao longo do eixo . Encontre equações paramétricas para a curva descrita por um ponto da circunferência que se encontra inicialmente na origem. (Esta curva é chamada ciclóide, veja a Figura 1(b))

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Seja uma função derivável e seja fixado. Verifique as afirmações são verdadeiras ou falsas. Justifique.

1. Se , para todo , então

Seja uma função derivável e seja fixado. Verifique as afirmações são verdadeiras ou falsas. Justifique.

1. Se é derivável até segunda ordem com e , para todo , então

Seja uma função derivável e seja fixado. Verifique as afirmações são verdadeiras ou falsas. Justifique.

d) se existe uma assíntota para (quando ) com coeficiente angular e se existe , então

Seja uma função derivável e seja fixado. Verifique as afirmações são verdadeiras ou falsas. Justifique.

1. Se então

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule a área da região entre os gráficos das funções e e as retas e

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Calcule as integrais indefinidas abaixo:

Desenhe a região e calcule sua área:

Desenhe a região e calcule sua área:

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem

Seja uma função derivável e seja fixado. Verifique as afirmações são verdadeiras ou falsas. Justifique.

e) se , então tem uma assíntota com coeficiente angular igual a

Determine a área da região plana delimitada pela curva e por sua reta tangente no ponto de abscissa

A reta horizontal intercepta a curva no primeiro quadrante como mostra a figura.

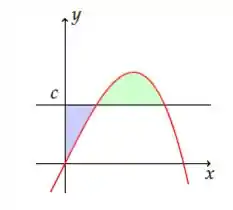
Determine para que as áreas das duas regiões sombreadas sejam iguais.

Calcule , interpretando-a como uma área

Calcule a área da região compreendida entre os gráficos de e , com

A região limitada pelas curvas e no primeiro quadrante é rotacionada em torno do eixo . Calcule o volume do sólido obtido

Calcule

Determine para que a área delimitada por e a reta seja igual a .

Encontre o volume de uma pirâmide cuja base é o quadrado de lado e cuja altura é .

Calcule o volume do sólido cuja base é a astróide de equação e tal que as seções transversais por planos paralelos ao plano são quadrados.

Calcule o comprimento do gráfico de , para .

Calcule a área da região do plano limitada pela elipse .

Calcule o volume da região do espaço limitada pelo elipsoide .

Mostre que é constante em . Qual o valor dessa constante?

Calcule o volume de uma calota esférica de altura , , de uma esfera de raio .

Calcule o valor da integral

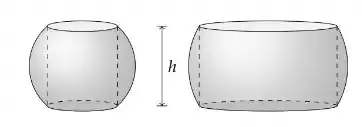
Um anel esférico é o sólido que permanece após a perfuração de um buraco cilíndrico através do centro de uma esfera sólida. Se a esfera tem raio R e o anel esférico tem altura h, prove o fato notável de que o volume do anel depende de h, mas não de R.

Calcule o volume do sólido obtido pela rotação em torno da reta da região delimitada pelas

parábolas

Determine o volume do sólido obtido pela rotação em torno do eixo do conjunto

Determine o volume do sólido obtido pela rotação em torno do eixo do conjunto

Determine o volume do sólido obtido pela rotação em torno do eixo do conjunto

Determine o comprimento da curva

Sejam contínua com , para todo ,

e

tais que a área de A ∩ B seja igual a 23. Calcule

Seja uma função contínua em um intervalo e sejam e funções diferenciáveis cujos valores estão em . Prove que

A fórmula acima é conhecida como Regra de Leibniz.

Seja . Calcule em termos de F(2).

Calcule .

Seja . Mostre que , para todo .