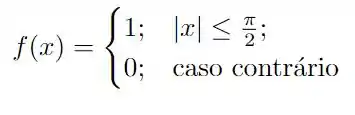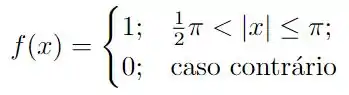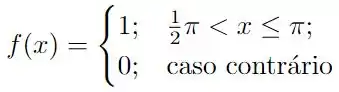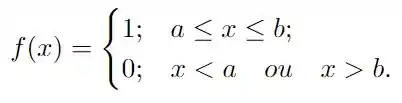Listas de EDB - Profª Aniura Milanés de Equações Diferenciais B da UFMG - Exercícios de EDB - 2021.1
Equações Diferenciais B - UFMG
Determine a ordem das equações a seguir. Classifique-as em lineares ou não lineares e especifique se cada equação linear é ou não homogênea.
;
Ver solução completaDetermine a ordem das equações a seguir. Classifique-as em lineares ou não lineares e especifique se cada equação linear é ou não homogênea.
;
Ver solução completaDetermine a ordem das equações a seguir. Classifique-as em lineares ou não lineares e especifique se cada equação linear é ou não homogênea.
;
Ver solução completaDetermine a ordem das equações a seguir. Classifique-as em lineares ou não lineares e especifique se cada equação linear é ou não homogênea.
;
Ver solução completaDetermine a ordem das equações a seguir. Classifique-as em lineares ou não lineares e especifique se cada equação linear é ou não homogênea.
;
Ver solução completaVerifique que as funções , , , são soluções da equação de Laplace bidimensional . Construa quatro novas soluções desta equação usando o Princípio de Superposição.
Ver solução completaObtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaObtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaObtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaObtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaObtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaObtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaObtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaObtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaObtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaObtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaObtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaObtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaObtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
com .
Ver solução completaObtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Ver solução completaSuponha que é uma função contínua com derivada contínua por partes.
Se , sob quais condições coincide com sua série de Fourier para todo satisfazendo
Ver solução completaSuponha que é uma função contínua com derivada contínua por partes.
Se , sob quais condições coincide com sua série de Fourier em senos para todo satisfazendo
Ver solução completaSuponha que é uma função contínua com derivada contínua por partes.
Se , sob quais condições coincide com sua série de Fourier em cossenos para todo satisfazendo
Ver solução completaConsidere a condução do calor em uma barra de comprimento cujas extremidades são mantidas à temperatura de para todo .
Em cada um dos casos a seguir, encontre uma expressão para a temperatura se a distribuição inicial de temperatura é a função dada. Determine se a condição inicial é satisfeita em todos os pontos e justifique. Explique em que sentido chamamos a expressão que você obteve de solução formal. Assuma que .
Ver solução completaConsidere a condução do calor em uma barra de comprimento cujas extremidades são mantidas à temperatura de para todo .
Em cada um dos casos a seguir, encontre uma expressão para a temperatura se a distribuição inicial de temperatura é a função dada. Determine se a condição inicial é satisfeita em todos os pontos e justifique. Explique em que sentido chamamos a expressão que você obteve de solução formal. Assuma que .
Ver solução completaConsidere a condução do calor em uma barra de comprimento cujas extremidades são mantidas à temperatura de para todo .
Em cada um dos casos a seguir, encontre uma expressão para a temperatura se a distribuição inicial de temperatura é a função dada. Determine se a condição inicial é satisfeita em todos os pontos e justifique. Explique em que sentido chamamos a expressão que você obteve de solução formal. Assuma que .
Ver solução completaConsidere a condução do calor em uma barra de comprimento cujas extremidades são mantidas à temperatura de para todo .
Em cada um dos casos a seguir, encontre uma expressão para a temperatura se a distribuição inicial de temperatura é a função dada. Determine se a condição inicial é satisfeita em todos os pontos e justifique. Explique em que sentido chamamos a expressão que você obteve de solução formal. Assuma que .
Ver solução completaConsidere o problema
ED
CF
CI
Onde é uma constante real.
Encontre a solução deste problema.
Ver solução completaConsidere o problema
ED
CF
CI
Onde é uma constante real.
A condição inicial é satisfeita?
Ver solução completaConsidere o problema
ED
CF
CI
Onde é uma constante real.
Determine para quais valores de existe quando , para todo .
Ver solução completaPara as equações diferenciais parciais a seguir, obtenha equações diferenciais ordinárias que devem satisfazer as funções para obtermos soluções fatoradas da forma .
Ver solução completaPara as equações diferenciais parciais a seguir, obtenha equações diferenciais ordinárias que devem satisfazer as funções para obtermos soluções fatoradas da forma .
Ver solução completaPara as equações diferenciais parciais a seguir, obtenha equações diferenciais ordinárias que devem satisfazer as funções para obtermos soluções fatoradas da forma .
Ver solução completaPara as equações diferenciais parciais a seguir, obtenha equações diferenciais ordinárias que devem satisfazer as funções para obtermos soluções fatoradas da forma .
Ver solução completaO aluno acha que entendeu o princípio de superposição e faz o seguinte raciocínio:
Como é solução da equação de Laplace bidimensional, então
também é.
Mas a aluna substitui a função na equação e obtém o seguinte.
Ou seja, não é solução da equação. Qual o erro de raciocínio de
Ver solução completaSem usar a fórmula obtida nas notas de aula, determine todas as soluções fatoradas da equação do calor
que se anulam quando e quando .
Ver solução completaComprove que as funções dadas são soluções das EDPs correspondentes.
, onde é uma constante.
Ver solução completaComprove que as funções dadas são soluções das EDPs correspondentes.
onde e são funções arbitrárias;
Ver solução completaComprove que as funções dadas são soluções das EDPs correspondentes.
onde e são funções arbitrárias.
Ver solução completaSe e são soluções da equação do calor, como você poderia construir infinitas soluções dessa equação usando as soluções acima?
Ver solução completaEscreve a forma geral das EDP’s lineares de segunda ordem com função incógnita . Quando a equação será homogênea? Por que você acha que eu não escrevi ela nas notas de aula?
Ver solução completaVerifique que a única função da forma satisfazendo é a função nula, calculando os coeficientes e e concluindo que eles devem ser nulos.
Ver solução completaVerdadeiro ou falso? Justifique.
A série de Fourier da função é obtida multiplicando cada termo na série de Fourier de por .
Ver solução completaOs coeficientes de Fourier de se calculam somando os coeficientes correspondentes de e de .
Ver solução completaOs coeficientes de Fourier de se calculam multiplicando os coeficientes correspondentes de e .
Ver solução completaObtenha as séries de Fourier das funções abaixo sem calcular nenhuma integral.
- ;
Obtenha as séries de Fourier das funções abaixo sem calcular nenhuma integral.
(b)
Ver solução completaObtenha as séries de Fourier das funções abaixo sem calcular nenhuma integral.
(c)
Ver solução completaObtenha as séries de Fourier das funções abaixo sem calcular nenhuma integral.
(d)
Ver solução completaPara todas as funções cuja séries de Fourier você calculou nos exercícios e e , e .
Explique por que estas funções satisfazem as hipóteses do teorema de convergência das séries de Fourier estudado nesta semana.
Ver solução completaPara todas as funções cuja séries de Fourier você calculou nos exercícios e e , e .
Em quais pontos do intervalo vale que ?
Ver solução completaPara todas as funções cuja séries de Fourier você calculou nos exercícios e e , e .
Esboce o gráfico de no intervalo
Ver solução completaVerifique as igualdades
; (1)
; (2)
; (3)
e
; (4)
. (5)
utilizando as identidades trigonométricas a seguir
(6)
(7)
; (8)
; (9)
. (10)
Ver solução completaConsidere a equação diferencial ordinária
Determine os valores de para os quais existem soluções não nulas desta equação que satisfazem as condições de fronteira abaixo. Obtenha também a expressão destas soluções. Considere .
, .
Ver solução completaConsidere a equação diferencial ordinária
Determine os valores de para os quais existem soluções não nulas desta equação que satisfazem as condições de fronteira abaixo. Obtenha também a expressão destas soluções. Considere .
, .
Ver solução completaUtilize o item do exercício anterior para determinar todas as soluções fatoradas não nulas da equação do calor satisfazendo as condições de fronteira para o problema
ED , , ;
CF , , ;
CI , .
Ver solução completaDetermine a solução do problema de condução do calor
A solução obtida satisfaz a condição inicial?
Ver solução completaConsidere a equação
Verifique que para constantes arbitrárias e , as funções e também são soluções da equação.
Ver solução completaConsidere a equação
Comprove que não é solução da equação. Sugestão: Verifique que
Ver solução completaO problema a seguir
,
.
descreve a propagação do calor numa barra de comprimento cujas extremidades também foram isoladas termicamente.
Se for uma solução fatorada da equação, satisfazendo as condições de fronteira acima, qual é o problema de fronteira que a função deve satisfazer?
Ver solução completaO problema a seguir
,
.
descreve a propagação do calor numa barra de comprimento cujas extremidades também foram isoladas termicamente.
Para quais valores de esse problema tem solução? Determine essas soluções.
Ver solução completaO problema a seguir
,
.
descreve a propagação do calor numa barra de comprimento cujas extremidades também foram isoladas termicamente.
Obtenha as soluções fatoradas que você precisaria usar para resolver esse problema usando o método de separação de variáveis.
Ver solução completaDetermine a série de Fourier das funções a seguir.
estendida de forma -periódica;
Ver solução completaPara cada uma das funções abaixo, definidas no intervalo , obtenha sua série de Fourier e esboce seu gráfico no intervalo .
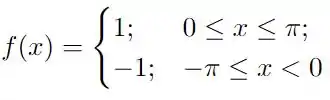
Para cada uma das funções abaixo, definidas no intervalo , obtenha sua série de Fourier e esboce seu gráfico no intervalo .
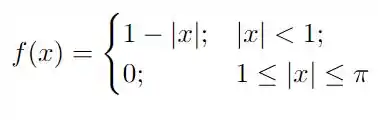
Assumindo que e estão definidas em , verifique que é ímpar se é par e viceversa.
Ver solução completaVerifique que para qualquer valor de , a função satisfaz a equação da onda unidimensional .
Ver solução completaUtilize a identidade para escrever como superposição de ondas viajando à esquerda e à direita com velocidade .
Ver solução completaVerifique que todas as funções que sejam polinômios de e de primeira ordem satisfazem a equação de Laplace. (ou seja, são funções harmônicas).
Ver solução completaVerifique que qualquer função de forma satisfaz a equação de Laplace. Aqui e são constantes arbitrárias.
Ver solução completaDetermine condições sobre as constantes e para que o polinômio homogêneo de segunda ordem satisfaça a equação de Laplace.
Ver solução completaSejam e funções harmônicas (i.e soluões da equação de Laplace).
Prove que também é uma função harmônica para quaisquer .
Ver solução completaSejam e funções harmônicas (i.e soluões da equação de Laplace).
Se é harmônica, prove que é harmônica, se e somente se, , para e constantes.
Ver solução completaSejam e funções harmônicas (i.e soluões da equação de Laplace).
Dê um exemplo de duas funções harmônicas cujo produto não seja uma função harmônica.
Ver solução completaEscreva o problema de Dirichlet para a equação de Laplace satisfeito pela função no quadrado unitário
Ver solução completaUtilizando o exercício anterior, para cada uma das funções especificadas a seguir, determine a função harmônica fora do círculo , que coincide com a função dada sobre a circunferência .
com constante.
Ver solução completaUtilizando o exercício anterior, para cada uma das funções especificadas a seguir, determine a função harmônica fora do círculo , que coincide com a função dada sobre a circunferência .
Ver solução completaUtilizando o exercício anterior, para cada uma das funções especificadas a seguir, determine a função harmônica fora do círculo , que coincide com a função dada sobre a circunferência .
Ver solução completaUtilizando o exercício anterior, para cada uma das funções especificadas a seguir, determine a função harmônica fora do círculo , que coincide com a função dada sobre a circunferência .
Ver solução completaDetermine a forma complexa das séries de Fourier das funções a seguir, definidas no intervalo [−π, π].
Ver solução completa
Determine a forma complexa das séries de Fourier das funções a seguir, definidas no intervalo [−π, π].
Ver solução completa
Seja
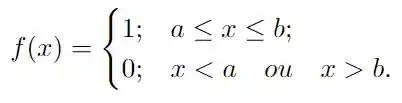
Qual relação deve haver entre e para que a parte imaginária de valha zero para qualquer calor de ?
Ver solução completaSuponha que definimos a transformada de Fourier pela expressão
Qual será neste caso a fórmula para a transformada de Fourier inversa?
Ver solução completaDetermine a transformada de Fourier das funções a seguir utilizando a tabela de transformadas vista em sala de aula.
Ver solução completaDetermine a transformada de Fourier das funções a seguir utilizando a tabela de transformadas vista em sala de aula.
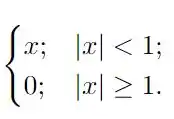
Determine a transformada de Fourier das funções a seguir utilizando a tabela de transformadas vista em sala de aula.
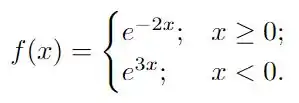
Determine a transformada de Fourier das funções a seguir utilizando a tabela de transformadas vista em sala de aula.
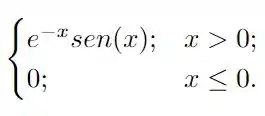
Determine a transformada de Fourier inversa das funções a seguir utilizando a tabela de transformadas vista em sala de aula.
Ver solução completaDetermine a transformada de Fourier inversa das funções a seguir utilizando a tabela de transformadas vista em sala de aula.
Ver solução completaVerifique que todas as soluções fatoradas da equação do calor da forma
que satisfazem as condições de fronteira que representam extremidades isoladas devem ser nulas.
Ver solução completaUma barra metálica de comprimento com constante de difusividade térmica é isolada termicamente, incluindo seus extremos. Suponha que a distribuição inicial de temperatura é onde:
Escreva a expressão da temperatura no instante .
Ver solução completaSuponha que os extremos esquerdo e direito de uma barra homogênea são introduzidos em recipientes com líquidos a temperatura e , respectivamente. Utilizando a Lei de Resfriamento de Newton é possível deduzir que a densidade de fluxo de calor através das extremidades, deve satisfazer as igualdades:
onde e são constantes positivas que representam a condutividade térmica do material da barra e o coeficiente de transferência de calor, respectivamente entre o líquido e os extremos da barra.
Suponha que e são nulas, ou seja, ambos os líquidos estão sendo mantidos a temperatura zero.
a) Escreva o problema de valor inicial com condições de fronteira para a equação do calor que corresponda com a situação física descrita acima.
Ver solução completaSuponha que os extremos esquerdo e direito de uma barra homogênea são introduzidos em recipientes com líquidos a temperatura e , respectivamente. Utilizando a Lei de Resfriamento de Newton é possível deduzir que a densidade de fluxo de calor através das extremidades, deve satisfazer as igualdades:
onde e são constantes positivas que representam a condutividade térmica do material da barra e o coeficiente de transferência de calor, respectivamente entre o líquido e os extremos da barra.
Suponha que e são nulas, ou seja, ambos os líquidos estão sendo mantidos a temperatura zero.
Determine que condições de fronteira deve satisfazer para que uma solução fatorada da equação do calor satisfaça as condições de fronteira apresentadas acima.
Ver solução completaSuponha que os extremos esquerdo e direito de uma barra homogênea são introduzidos em recipientes com líquidos a temperatura e , respectivamente. Utilizando a Lei de Resfriamento de Newton é possível deduzir que a densidade de fluxo de calor através das extremidades, deve satisfazer as igualdades:
onde e são constantes positivas que representam a condutividade térmica do material da barra e o coeficiente de transferência de calor, respectivamente entre o líquido e os extremos da barra.
Suponha que e são nulas, ou seja, ambos os líquidos estão sendo mantidos a temperatura zero.
c) Qual seria a maior dificuldade para resolver o problema em ?
Ver solução completaSuponha que os extremos esquerdo e direito de uma barra homogênea são introduzidos em recipientes com líquidos a temperatura e , respectivamente. Utilizando a Lei de Resfriamento de Newton é possível deduzir que a densidade de fluxo de calor através das extremidades, deve satisfazer as igualdades:
onde e são constantes positivas que representam a condutividade térmica do material da barra e o coeficiente de transferência de calor, respectivamente entre o líquido e os extremos da barra.
Suponha que e são nulas, ou seja, ambos os líquidos estão sendo mantidos a temperatura zero.
d) Determine a solução estacionária do problema que você escreveu em (a).
Ver solução completaResolva o problema
Nos casos seguintes. Em cada caso, calcule a razão entre a amplitude dos dois primeiros harmônicos que aparecem na solução.
a)
Ver solução completaResolva o problema
Nos casos seguintes. Em cada caso, calcule a razão entre a amplitude dos dois primeiros harmônicos que aparecem na solução.
b)
Ver solução completaResolva o problema
Nos casos seguintes. Em cada caso, calcule a razão entre a amplitude dos dois primeiros harmônicos que aparecem na solução.
c) .
Ver solução completa