Listas de Cálculo 1 - UNICAMP de Cálculo 1 da UNICAMP - Lista 3 - Limite e Continuidade
Cálculo 1 - UNICAMP
17. Devido a sua conexão com retas secante, tangente e taxas instantâneas, os limites da forma
Ocorrem com frequência em cálculo. Avalie os seguintes limites para os valores dados de e a função .
a)
Ver solução completa17. Devido a sua conexão com retas secante, tangente e taxas instantâneas, os limites da forma
Ocorrem com frequência em cálculo. Avalie os seguintes limites para os valores dados de e a função .
b)
Ver solução completa17. Devido a sua conexão com retas secante, tangente e taxas instantâneas, os limites da forma
Ocorrem com frequência em cálculo. Avalie os seguintes limites para os valores dados de e a função .
c)
Ver solução completa17. Devido a sua conexão com retas secante, tangente e taxas instantâneas, os limites da forma
Ocorrem com frequência em cálculo. Avalie os seguintes limites para os valores dados de e a função .
d)
Ver solução completa22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
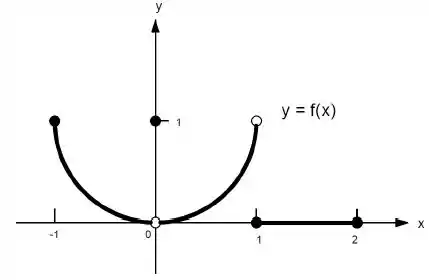
a)
Ver solução completa22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
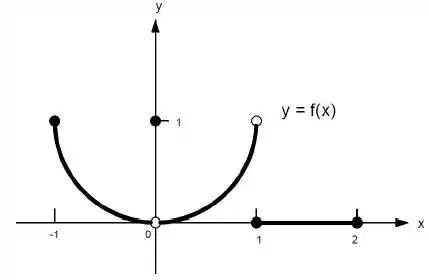
b)
Ver solução completa22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
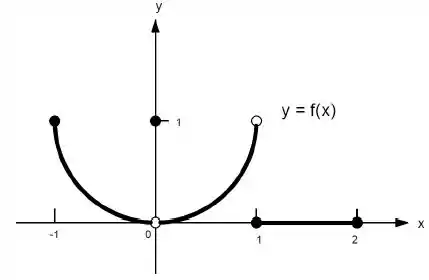
c)
Ver solução completa22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
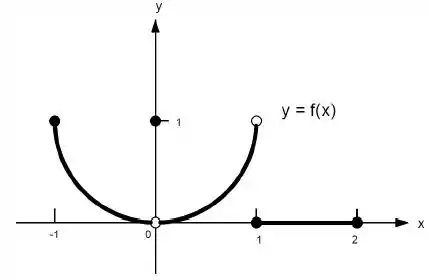
d)
Ver solução completa22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
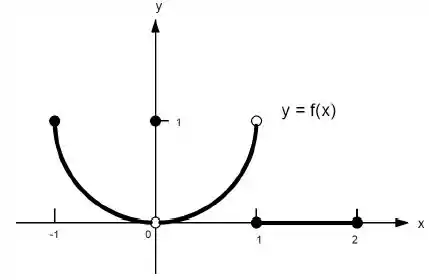
e) existe
Ver solução completa22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
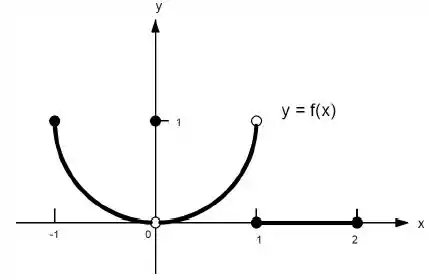
f)
Ver solução completa22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
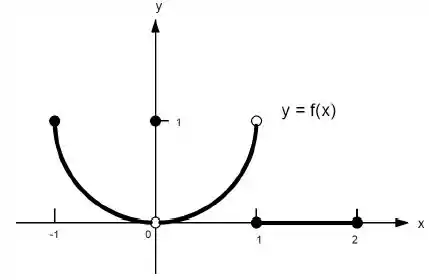
g)
Ver solução completa22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
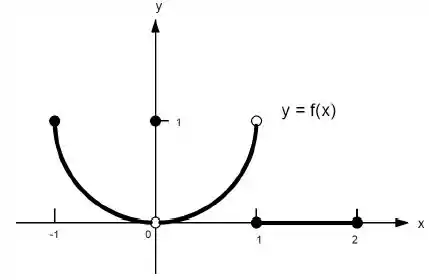
h)
Ver solução completa22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
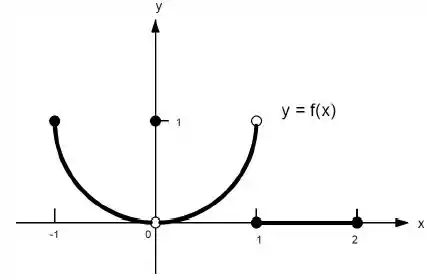
i)
Ver solução completa22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
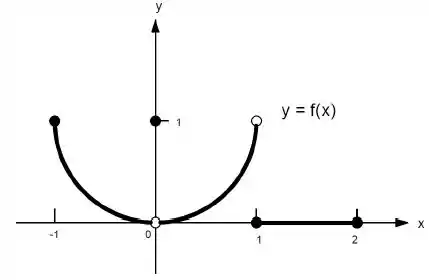
j)
Ver solução completa13. Suponha que e . Especifique quais regras do teorema abaixo utilizadas para efetuar as etapas 1, 2 e 3 do cálculo a seguir:
Teorema (Leis do Limite). Se e são números reais e
e ,
Então:
1.
2.
3.
4.
5.
6. onde
7. , onde
Ver solução completa14. Suponha que , e . Especifique quais regras do teorema abaixo utilizadas para efetuar as etapas 1, 2 e 3 do cálculo a seguir:
Teorema (Leis do Limite). Se e são números reais e
e ,
Então:
1.
2.
3.
4.
5.
6. onde
7. , onde
Ver solução completa22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
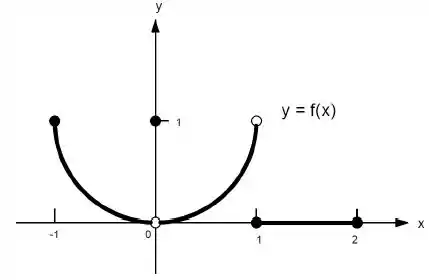
k) não existe
Ver solução completa22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
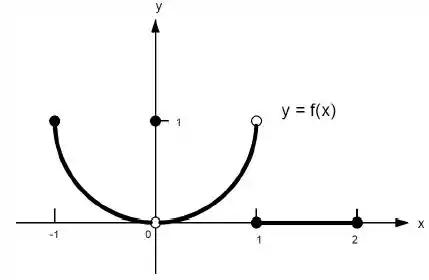
k)
Ver solução completa23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
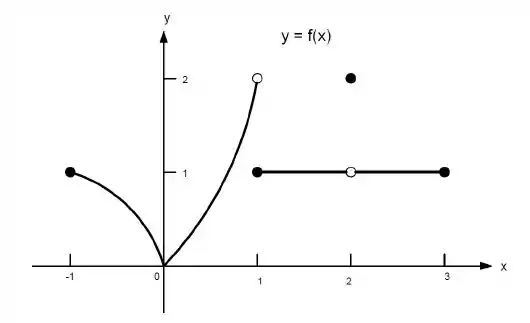
a)
Ver solução completa23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
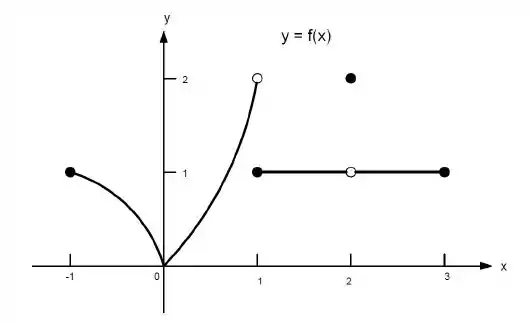
b) não existe
Ver solução completa23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
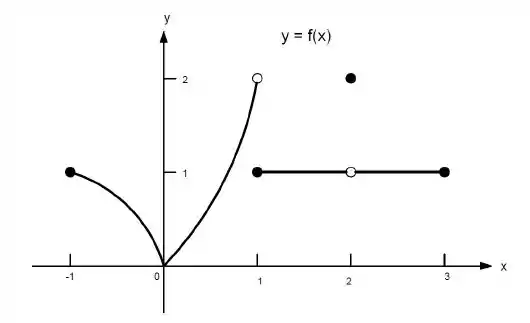
c)
Ver solução completa23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
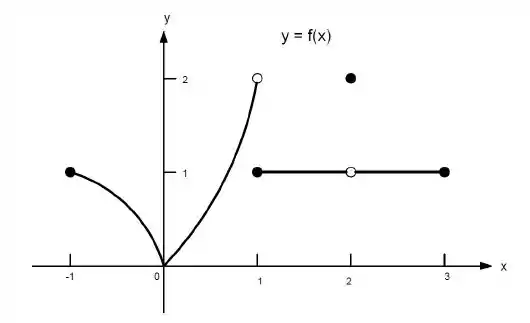
d)
Ver solução completa23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
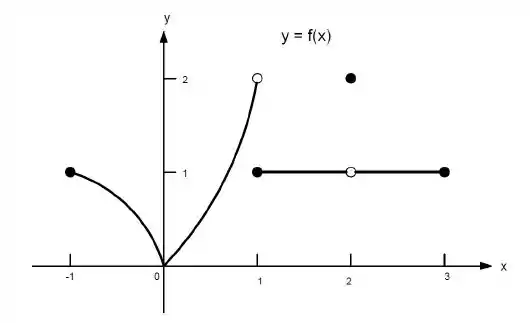
e)
Ver solução completa23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
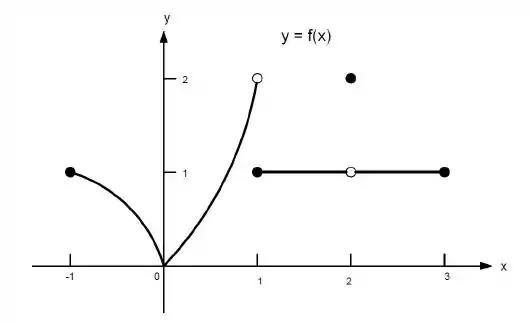
f)
Ver solução completa23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
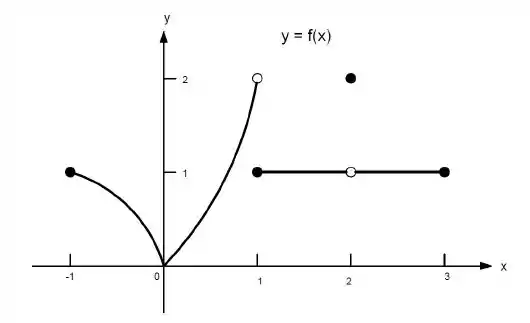
g) não existe
Ver solução completa23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
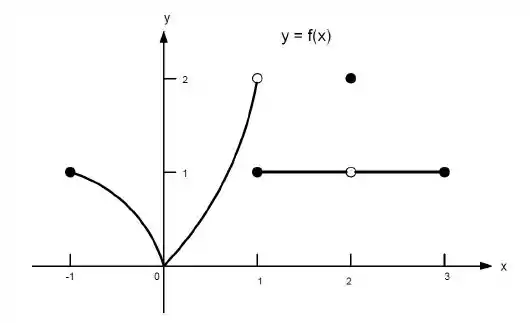
h) existe para qualquer no intervalo aberto .
Ver solução completa23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
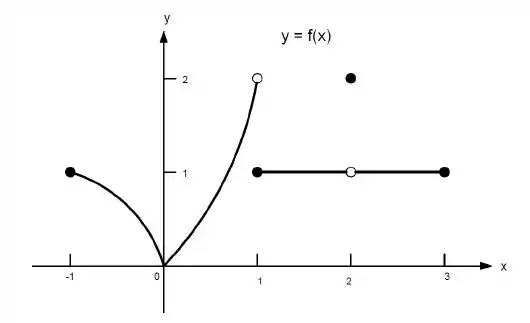
i) existe para qualquer no intervalo aberto .
Ver solução completa23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
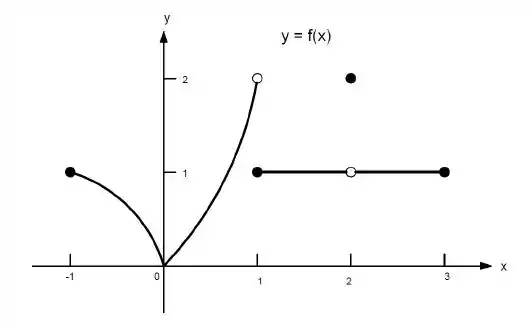
j)
Ver solução completa23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
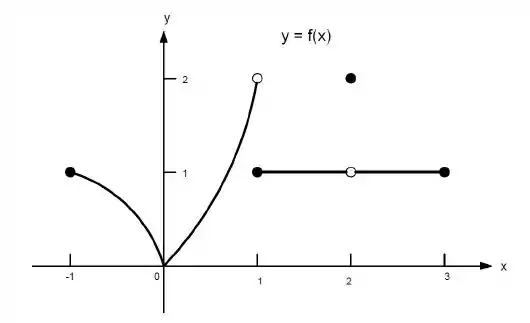
k) não existe.
Ver solução completa52. Utilize limites para determinar as equações para todas as assíntotas horizontais.
a)
Ver solução completa52. Utilize limites para determinar as equações para todas as assíntotas horizontais.
b)
Ver solução completa52. Utilize limites para determinar as equações para todas as assíntotas horizontais.
c)
Ver solução completa52. Utilize limites para determinar as equações para todas as assíntotas horizontais.
d)
Ver solução completa9. Suponhamos que a função seja definida para todo em . O que pode ser dito sobre a existência de . Justifique sua resposta.
Ver solução completa10. Se , deve existir? Em caso afirmativo, deve ser ? Podemos concluir algo sobre ? Explique.
Ver solução completa18. Nos exercícios de a) - f), esboce o intervalo no eixo com o ponto dentro. Em seguida, determine um valor de , de modo que para todo ,
a)
Ver solução completa18. Nos exercícios de a)-f), esboce o intervalo no eixo com o ponto dentro. Em seguida, determine um valor de , de modo que para todo ,
b)
Ver solução completa18. Nos exercícios de a)-f), esboce o intervalo no eixo com o ponto dentro. Em seguida, determine um valor de , de modo que para todo ,
c)
Ver solução completa18. Nos exercícios de a)-f), esboce o intervalo no eixo com o ponto dentro. Em seguida, determine um valor de , de modo que para todo ,
d)
Ver solução completa18. Nos exercícios de a)-f), esboce o intervalo no eixo com o ponto dentro. Em seguida, determine um valor de , de modo que para todo ,
e)
Ver solução completa18. Nos exercícios de a)-f), esboce o intervalo no eixo com o ponto dentro. Em seguida, determine um valor de , de modo que para todo ,
f)
Ver solução completa26. Faça o gráfico da função e em seguida, responda:
a) Qual é o domínio e a imagem de ?
Ver solução completa26. Faça o gráfico da função e em seguida, responda:
b) Em quais pontos , se houver, existe?
Ver solução completa26. Faça o gráfico da função e em seguida, responda:
c) Em quais pontos existe o limite à esquerda?
Ver solução completa26. Faça o gráfico da função e em seguida, responda:
d) Em quais pontos existe o limite à direita?
Ver solução completa27. Explique o que significa dizer que e .
Nesta situação, é possível que exista? Explique.
Ver solução completa32. Dê exemplo de uma função definida em e que seja contínua em todos os pontos, exceto em
Ver solução completa1. Um tanque com capacidade para 1000 litros de água é drenado pela base em meia hora. Os valores na tabela mostram o volume de água remanescente no tanque (em litros) após minutos.
a) Se é o ponto sobre o gráfico de , encontre as inclinações das retas secantes , onde é o ponto sobre o gráfico com e .
Ver solução completa1. Um tanque com capacidade para 1000 litros de água é drenado pela base em meia hora. Os valores na tabela mostram o volume de água remanescente no tanque (em litros) após minutos.
b) Estime a inclinação da reta tangente em pela média das inclinações de duas retas secantes.
Ver solução completa1. Um tanque com capacidade para 1000 litros de água é drenado pela base em meia hora. Os valores na tabela mostram o volume de água remanescente no tanque (em litros) após minutos.
c) Use um gráfico da função para estimar a inclinação da tangente em . (Essa inclinação representa a razão na qual a água flui do tanque após 15 minutos.)
Ver solução completa2. O ponto está sobre a curva .
a) se é o ponto , use sua calculadora para determinar a inclinação da reta secante , com precisão de seis casas decimais, para os seguintes valores:
a) 1,5
b) 1,9
c) 1,99
d) 1,999
e) 2,5
f) 2,1
g) 2,01
h) 2,001
Ver solução completa2. O ponto está sobre a curva .
b) Usando os resultados da parte (a), estime o valor da inclinação da reta tangente à curva no ponto .
Ver solução completa2. O ponto está sobre a curva .
c) Usando a inclinação da parte (b), encontre uma equação da reta tangente à curva em .
Ver solução completa3. Determine o coeficiente angular da curva no ponto dado e uma equação da reta tangente em .
a) ,
Ver solução completa3. Determine o coeficiente angular da curva no ponto dado e uma equação da reta tangente em .
b)
Ver solução completa3. Determine o coeficiente angular da curva no ponto dado e uma equação da reta tangente em .
c)
Ver solução completa3. Determine o coeficiente angular da curva no ponto dado e uma equação da reta tangente em .
d)
Ver solução completa3. Determine o coeficiente angular da curva no ponto dado e uma equação da reta tangente em .
e)
Ver solução completa3. Determine o coeficiente angular da curva no ponto dado e uma equação da reta tangente em .
f)
Ver solução completa4. Nos exercícios de a) – f), determine a taxa de variação média da função nos intervalos dados.
a) a., b.
Ver solução completa4. Nos exercícios de a) – f) , determine a taxa de variação média da função nos intervalos dados.
b) a., b.
Ver solução completa4. Nos exercícios de a) – f) , determine a taxa de variaç��o média da função nos intervalos dados.
c) a., b.
Ver solução completa4. Nos exercícios de a) – f) , determine a taxa de variação média da função nos intervalos dados.
d) a., b.
Ver solução completa4. Nos exercícios de a) – f) , determine a taxa de variação média da função nos intervalos dados.
e)
Ver solução completa4. Nos exercícios de a) – f) , determine a taxa de variação média da função nos intervalos dados.
f)
Ver solução completa5. Faça uma tabela de valores para a função nos pontos , , , , e .
a) Determine a taxa média de variação de nos intervalos para cada em sua tabela.
Ver solução completa5. Faça uma tabela de valores para a função nos pontos , , , , e .
b) Amplie a tabela, se necessário, para tentar determinar a taxa de variação de em .
Ver solução completa6. Seja para .
a) Determine a taxa de variação média de com relação a nos intervalos , e .
Ver solução completa6. Seja para .
b) Faça uma tabela de valores da taxa média de variação de com relação a no intervalo para alguns valores de que se aproximem de zero, como e .
Ver solução completa6. Seja para .
c) O que sua tabela indica é a taxa de variação de com relação a em ?
Ver solução completa6. Seja para .
d) Calcule o limite, quando se aproxima de zero da taxa de variação média de com relação a no intervalo .
Ver solução completa7. Seja para .
a) Determine a taxa de variação média de com relação a nos intervalos
i) de a
ii) de a
Ver solução completa7. Seja para .
b) Faça uma tabela de valores de taxa média de variação de com relação a no intervalo , para alguns valores de que se aproximem de 2, como e .
Ver solução completa7. Seja para .
c) O que a sua tabela indica é a taxa média de variação de com relação a em ?
Ver solução completa7. Seja para .
d) Calcule o limite, quando se aproxima de 2, da taxa média de variação de com relação a no intervalo de a . Você precisará fazer alguns cálculos algébricos antes de substituir .
Ver solução completa37. Sejam e duas funções com mesmo domínio tais que e para todo em , onde é um número real fixo. Prove que
Ver solução completa44. Empregue o Teorema do Confronto para mostrar que
Ilustre, fazendo os gráficos das funções e (como no Teorema do Confronto) na mesma tela.
Ver solução completa51. Utilize limites para determinar as equações para todas as assíntotas verticais.
a)
Ver solução completa51. Utilize limites para determinar as equações para todas as assíntotas verticais.
b)
Ver solução completa51. Utilize limites para determinar as equações para todas as assíntotas verticais.
c)
Ver solução completa19. Cada um dos exercícios a) - h) dá uma função e números , e . Em cada caso, determine um intervalo aberto em torno de em que a desigualdade seja verdadeira. Dê então um valor para tal que, para todo satisfazendo , a desigualdade seja verdadeira.
a) , , ,
Ver solução completa19. Cada um dos exercícios a) - h) dá uma função e números , e . Em cada caso, determine um intervalo aberto em torno de em que a desigualdade seja verdadeira. Dê então um valor para tal que, para todo satisfazendo , a desigualdade seja verdadeira.
b) , , ,
Ver solução completa19. Cada um dos exercícios a) - h) dá uma função e números , e . Em cada caso, determine um intervalo aberto em torno de em que a desigualdade seja verdadeira. Dê então um valor para tal que, para todo satisfazendo , a desigualdade seja verdadeira.
c) , , ,
Ver solução completa19. Cada um dos exercícios a) - h) dá uma função e números , e . Em cada caso, determine um intervalo aberto em torno de em que a desigualdade seja verdadeira. Dê então um valor para tal que, para todo satisfazendo , a desigualdade seja verdadeira.
d) , , ,
Ver solução completa19. Cada um dos exercícios a) - h) dá uma função e números , e . Em cada caso, determine um intervalo aberto em torno de em que a desigualdade seja verdadeira. Dê então um valor para tal que, para todo satisfazendo , a desigualdade seja verdadeira.
e) , , ,
Ver solução completa19. Cada um dos exercícios a) - h) dá uma função e números , e . Em cada caso, determine um intervalo aberto em torno de em que a desigualdade seja verdadeira. Dê então um valor para tal que, para todo satisfazendo , a desigualdade seja verdadeira.
f) , , ,
Ver solução completa19. Cada um dos exercícios a) - h) dá uma função e números , e . Em cada caso, determine um intervalo aberto em torno de em que a desigualdade seja verdadeira. Dê então um valor para tal que, para todo satisfazendo , a desigualdade seja verdadeira.
g) , , , ,
Ver solução completa19. Cada um dos exercícios a) - h) dá uma função e números , e . Em cada caso, determine um intervalo aberto em torno de em que a desigualdade seja verdadeira. Dê então um valor para tal que, para todo satisfazendo , a desigualdade seja verdadeira.
h) , , , ,
Ver solução completaCada um dos exercícios a) - d) dá uma função , um ponto e um número positivo . Determine . Em seguida, determine um número δ > 0 de modo que para todo x
a.
Ver solução completaCada um dos exercícios a) - d) dá uma função , um ponto e um número positivo . Determine . Em seguida, determine um número δ > 0 de modo que para todo x
b.
Ver solução completaCada um dos exercícios a) - d) dá uma função , um ponto e um número positivo . Determine . Em seguida, determine um número δ > 0 de modo que para todo x
c.
Ver solução completaCada um dos exercícios a) - d) dá uma função , um ponto e um número positivo . Determine . Em seguida, determine um número δ > 0 de modo que para todo x
d.
Ver solução completaDetermine L para que a função seja contínua no ponto dado. Justifique.
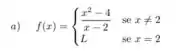
em p = 2
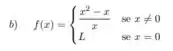
em p = 0
Ver solução completa