Listas de C1 - Profº Jair de Cálculo 1 da UFRJ - Primeira Edição V1.3
Cálculo 1 - UFRJ
Encontre uma equação para a que passa por:
g) e é paralela à reta que passa por e .
Ver solução completaUm cilindro fechado tem área de superfície fixa . Exprima seu volume como função do raio da base do cilindro.
Ver solução completaO perímetro de um triângulo retângulo é e a hipotenusa é . Exprima a área do triângulo como função de .
Ver solução completaDetermine o valor da constante para que a função , dada abaixo, seja contínua em .
Ver solução completaDetermine os valores das constantes e para que a função , dada abaixo, seja contínua em .
Ver solução completaDada a função para , defina o valor de para que a função seja contínua em , se para .
Ver solução completaDetermine o valor da constante para que a função , dada abaixo, seja contínua em .
Ver solução completaDetermine o valor da constante para que a função , dada abaixo, seja contínua em .
Ver solução completaDetermine o valor da constante para que a função , dada abaixo, seja contínua em .
Ver solução completaEncontre os valores de , e para que os gráficos das funções definidas por e se interceptem no ponto e tenham a mesma reta tangente neste ponto.
Ver solução completaSeja uma função diferenciável num intervalo . Considere a função .
(a) é contínua em ? Justifique.
Ver solução completaSeja uma função diferenciável num intervalo . Considere a função .
(b) Determine o valor de para que seja diferenciável em . Justifique.
Ver solução completaConsidere a função .
(a) Qual o maior conjunto onde a função inversa existe? Justifique.
Ver solução completaMostre que para é invertível e calcule . Encontre a equação da reta tangente ao gráfico de no ponto .
Ver solução completaConsidere para .
(b) Encontre a equação da reta tangente ao gráfico de no ponto .
Ver solução completaSeja . Mostre que é invertível para todo e calcule a derivada da função inversa em .
Ver solução completaSuponha que e são funções diferenciáveis no ponto e que e . Se e atingem um valor máximo local em , então mostre que também atingem um valor máximo local em .
Ver solução completaSeja uma função definida em , contínua em todo o seu domínio e satisfazendo as condições abaixo:
e
Suponha que o gráfico de é dado pela figura abaixo:
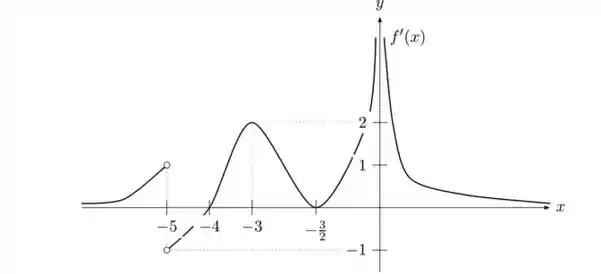
Responda, justificando, o que se pede:
Os intervalos onde é crescente, e onde é decrescente.
Ver solução completaSeja uma função definida em , contínua em todo o seu domínio e satisfazendo as condições abaixo:
e
Suponha que o gráfico de é dado pela figura abaixo:
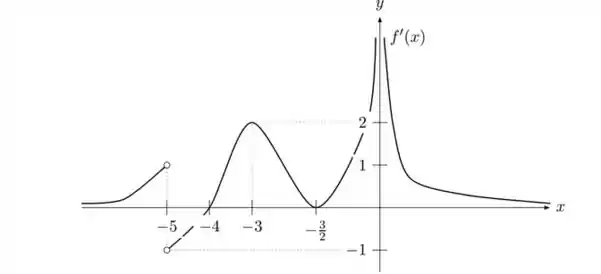
Responda, justificando, o que se pede:
Os pontos onde a reta tangente ao gráfico de é horizontal;
Ver solução completaSeja uma função definida em , contínua em todo o seu domínio e satisfazendo as condições abaixo:
e
Suponha que o gráfico de é dado pela figura abaixo:
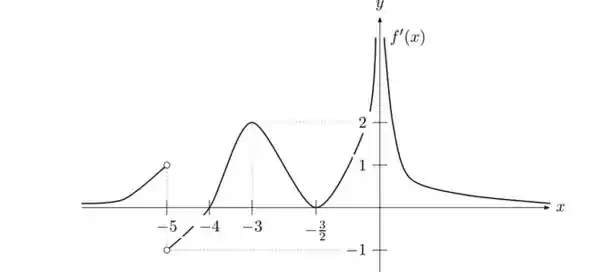
Responda, justificando, o que se pede:
c) Os pontos de máximos e mínimos relativos (locais) caso existam;
Ver solução completaSeja uma função definida em , contínua em todo o seu domínio e satisfazendo as condições abaixo:
e
Suponha que o gráfico de é dado pela figura abaixo:
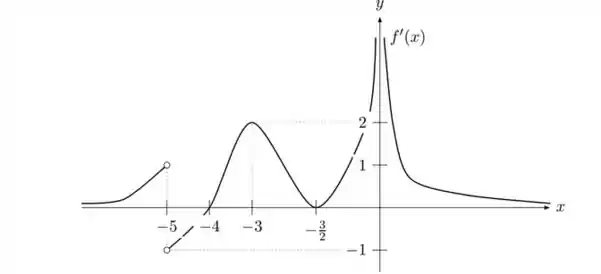
Responda, justificando, o que se pede:
os intervalos onde o gráfico de possui concavidade para cima e onde possui concavidade para baixo.
Ver solução completaSeja uma função definida em , contínua em todo o seu domínio e satisfazendo as condições abaixo:
e
Suponha que o gráfico de é dado pela figura abaixo:
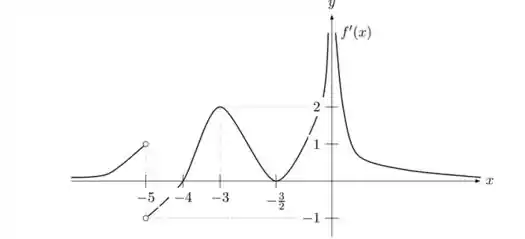
Responda, justificando, o que se pede:
os pontos de inflexão, caso existam;
Ver solução completaSeja uma função definida em , contínua em todo o seu domínio e satisfazendo as condições abaixo:
e
Suponha que o gráfico de é dado pela figura abaixo:
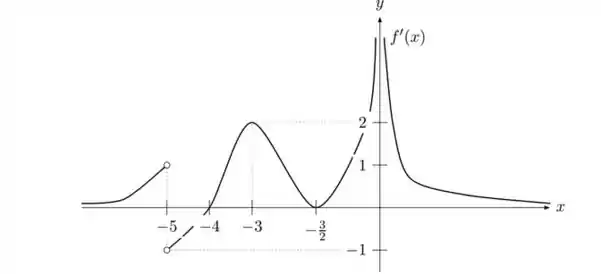
Responda, justificando, o que se pede:
As assíntotas verticais e horizontais, caso existam;
Ver solução completaEsboce os gráficos das funções abaixo indicando: o domínio; as assíntotas, caso existam; os intervalos de crescimento e decrescimento; os extremos relativos e absolutos, caso existam; os intervalos onde o gráfico possui concavidade para cima e para baixo; os pontos de inflexão, caso existam.
Ver solução completaSeja uma função contínua em tal que:
Suponha que o gráfico de seja dada pela figura abaixo:
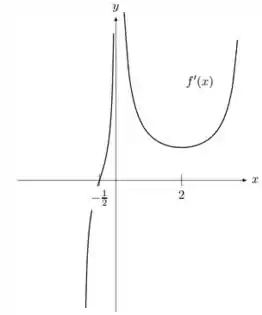
Responde o que se pede:
a) Os intervalos onde é crescente, e onde é decrescente.
Ver solução completaSeja uma função contínua em tal que:
Suponha que o gráfico de seja dada pela figura abaixo:
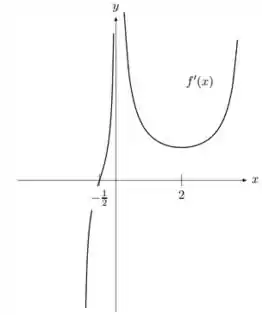
Responde o que se pede:
Os pontos onde a reta tangente ao gráfico de é horizontal;
Ver solução completaSeja uma função contínua em tal que:
Suponha que o gráfico de seja dada pela figura abaixo:
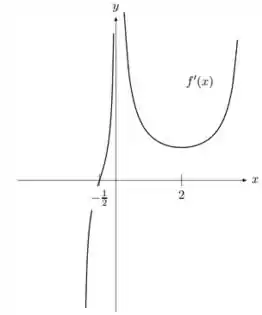
Responde o que se pede:
c) Os pontos de máximos e mínimos relativos (locais) caso existam;
Ver solução completaSeja uma função contínua em tal que:
Suponha que o gráfico de seja dada pela figura abaixo:
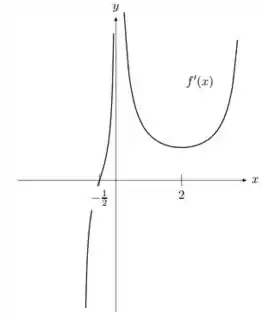
Responde o que se pede:
os intervalos onde o gráfico de possui concavidade para cima e onde possui concavidade para baixo.
Ver solução completaSeja uma função contínua em tal que:
Suponha que o gráfico de seja dada pela figura abaixo:
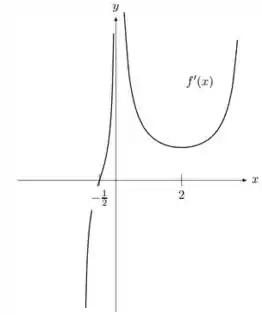
Responde o que se pede:
os pontos de inflexão, caso existam;
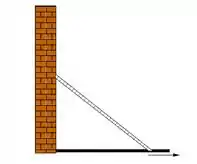
Ver solução completaUma escada com de comprimento está apoiada numa parede vertical. Se a base da escada for puxada horizontalmente, afastando-se da parede a , qual a velocidade com que a parte superior da escada estará deslizando ao longo da parede, quando a sua base estiver a da parede?
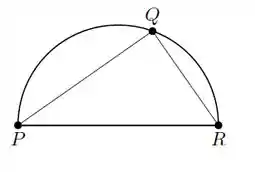
Um triângulo está inscrito num semicírculo de diâmetro conforme a figura abaixo. Sabendo que o vértice varia sobre o semicírculo e que o lado aumenta à razão de , determine a taxa com a qual a área do triângulo varia no instante em que o lado mede .
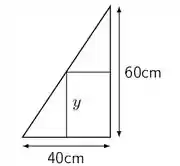
Um retângulo possui lados que variam com o tempo e está inscrito numa região triangular conforme a figura abaixo. Determine com que taxa a área do retângulo está variando no instante em que sua altura mede e está aumentando à taxa de . Nesse instante a área está aumentando ou diminuindo?
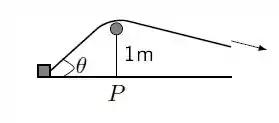
Uma caixa está sendo puxada por uma corda que passa por uma roldana presa a acima do solo. Determine a taxa de variação do ângulo , indicado na figura abaixo, no instante em que a caixa se encontra a do ponto , situado abaixo da roldada, sabendo que a caixa se desloca a .
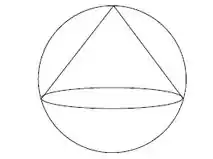
Um cone está inscrito em uma esfera conforme mostra figura abaixo. Se o raio da esfera está aumentando a uma taxa de e a altura do cone está aumentando a uma taxa de , com que taxa está aumentando o volume do cone no instante em que o raio da esfera mede e a altura do cone mede .
Dois carros, um dirigindo-se para o leste à razão de e o outro para o sul à razão de , estão viajando em direção à interseção das duas rodovias. À que razão os carros aproximam-se um do outro, no instante em que o primeiro (direção leste) estiver a e o segundo (direção sul) a da interseção?
Ver solução completaUm balão eleva-se verticalmente do solo à razão de . Quando o balão está a do solo, passa exatamente sob ele um automóvel viajando a velocidade de . Com que velocidade varia, (quatro) segundo após, a distância entre eles?
Ver solução completaQuando o último vagão de um trem passa por baixo de um viaduto, um carro cruza o viaduto numa rodovia perpendicular aos trilhos e a acima deles. O trem está a e o carro a . Com que velocidade se afastam um do outro após ?
Ver solução completaUm fusca viaja à razão de aproxima-se de um cruzamento. Quando o fusca está a do cruzamento um caminhão que viaja à razão de atravessa o cruzamento. O fusca e o caminhão estão em rodovias que formam um ângulo reto. Com que rapidez separam-se o fusca e o caminhão depois que o caminhão passou pelo cruzamento?
Ver solução completaDois lados paralelos de um retângulo aumentam à razão de , mas os outros dois lados diminuem de tal modo que a figura permaneça um retângulo de área constante igual a . Qual a velocidade com que o perímetro varia quando o lado que aumenta mede ?
Ver solução completaUm quadro de de altura é colocado em uma parede de tal forma que sua base esteja no mesmo nível dos olhos de um observador que está se aproximando da parede a uma velocidade de . Com que velocidade a medida do ângulo de visão do quadro estará variando quando o observador estiver a da parede?
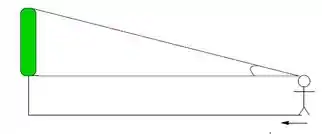
Uma calha horizontal possui de comprimento e tem como seção transversal um triângulo isósceles de de base e de altura conforme mostra a figura abaixo.
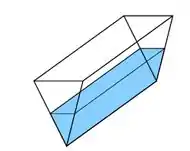
Devido à chuva, a água em seu interior está se elevando. Quão rápido o volume de água em seu interior estará aumentando no instante em que o nível da água for de e estiver aumentando a uma razão de .
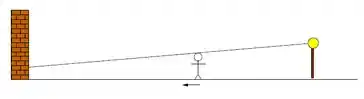
Ver solução completaUma mulher de de altura caminha em direção a um muro a uma razão de . Diretamente atrás dela e a do muro está um refletor acima do nível do solo.
Quão rápido o comprimento da sombra da mulher estará variando no muro quando ela estiver a meio caminho entre o refletor e o muro? A sombra está esticando-se ou encurtando-se?
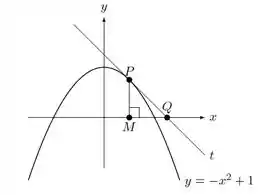
Considere a parábola na figura abaixo, onde a reta é tangente à parábola no primeiro quadrante em cada ponto . Sabendo que a taxa de variação da abscissa de (coordenada ) é de , determine a taxa de variação do lado do triângulo , quando o ponto de tangência é .
Na figura abaixo, é o ponto de tangência da reta com a curva . Sabendo que o ponto se desloca sobre a curva mostre que:
(a) O triângulo é sempre isósceles.
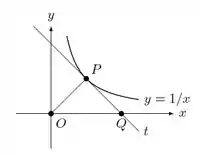
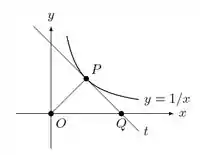
Na figura abaixo, é o ponto de tangência da reta com a curva . Sabendo que o ponto se desloca sobre a curva mostre que:
(b) A taxa de variaç��o da área do triângulo independe da velocidade com que o ponto se desloca.
Determine os valores das constantes e para que o gráfico da função e a curva definida implicitamente por tenham a mesma reta tangente no ponto .
Ver solução completaSeja uma função definida pela equação
(a) Encontre uma equação da reta tangente ao gráfico da curva no ponto .
Ver solução completaSeja uma função definida pela equação
(b) Existem pontos dessa curva onde a reta tangente é vertical? Justifique.
Ver solução completaDetermine o volume do sólido gerado pela rotação, em torno do eixo , da região limitada pela curva e pelas retas , e .
Ver solução completaCalcule o volume do sólido obtido pela rotação, em torno da reta , da região limitada pelas curvas e , para .
Ver solução completaConsidere o sólido gerado pela rotação, em torno do eixo , da região limitada pela parábola e a reta , com . Determine o valor de se o volume deste sólido é .
Ver solução completaPara cada , seja a região limitada pelo gráfico de , o eixo e a reta . Se é o volume obtido girando em torno do eixo , e é o volume do sólido obtido girando-se em torno do eixo , determine .
Ver solução completaSeja a região infinita delimitada pelas curvas e , . Calcule o volume do sólido obtido pela rotação de em torno do eixo .
Ver solução completaEncontre o volume do sólido obtido pela rotação, em torno do eixo , da região infinita situada entre o gráfico de e sua assíntota horizontal.
Ver solução completaSuponha que dois ciclistas estão correndo com a mesma velocidade escalar, ambos partindo, ao mesmo tempo, do ponto . Sabendo que o ciclista percorre o arco de circunferência e o ciclista percorre o arco da curva para . Qual deles chegará primeiro ao ponto ?
Ver solução completa6. Seja para .
(b) Encontre a equação da reta tangente ao gráfico de no ponto .
Ver solução completa2. Esboce os gráficos das funções abaixo indicando: o domínio; as assíntotas, caso existam; os intervalos de crescimento e decrescimento; os extremos relativos e absolutos, caso existam; os intervalos onde o gráfico possui concavidade para cima e para baixo; os pontos de inflexão, caso existam.
(b)
Ver solução completa2. Esboce os gráficos das funções abaixo indicando: o domínio; as assíntotas, caso existam; os intervalos de crescimento e decrescimento; os extremos relativos e absolutos, caso existam; os intervalos onde o gráfico possui concavidade para cima e para baixo; os pontos de inflexão, caso existam.
(c)
Ver solução completa2. Esboce os gráficos das funções abaixo indicando: o domínio; as assíntotas, caso existam; os intervalos de crescimento e decrescimento; os extremos relativos e absolutos, caso existam; os intervalos onde o gráfico possui concavidade para cima e para baixo; os pontos de inflexão, caso existam.
(d)
Ver solução completa2. Esboce os gráficos das funções abaixo indicando: o domínio; as assíntotas, caso existam; os intervalos de crescimento e decrescimento; os extremos relativos e absolutos, caso existam; os intervalos onde o gráfico possui concavidade para cima e para baixo; os pontos de inflexão, caso existam.
(e)
Ver solução completa